본 글은 Udemy의 자바 자료구조 강의를 듣고 개인적으로 학습한 내용 복습하기 위해 작성된 글로 내용상 오류가 있을 수 있습니다. 오류가 있다면 지적 부탁 드리겠습니다.
1. Binary Search Tree란?
이진 탐색 트리는 이진탐색의 개념을 트리 형태의 구조에 접목한 자료구조이다.
1.1 Binary Search?
이진 탐색은 정렬된 데이터의 중간에 위치한 항목을 기준으로 데이터를 두 부분으로 나누어 가며 특정 항목을 탐색하는 방법이다.
1.2 Tree?
배열이나 연결리스트는 데이터를 일렬로 저장하기 때문에 탐색 연산이 순차적으로 수행되어야 한다는 단점을 가진다. 배열은 미리 정렬해 놓으면 이진탐색을 통해 효율적인 탐색이 가능하지만 삽입이나 삭제 후에도 정렬상태를 유지해야 하므로 삽입이나 삭제를 하는데 O(N) 시간이 소요된다. 이러한 문제를 보완한 것이 계층적 자료구조인 트리(Tree)이다.
트리는 실제 트리를 거꾸로 세워 놓은 형태의 자료구조로 HTML, XML, 자바 클래스 계층구조, 운영체제의 파일 시스템 등에서 쓰인다.
트리의 구성요소는 아래와 같다.
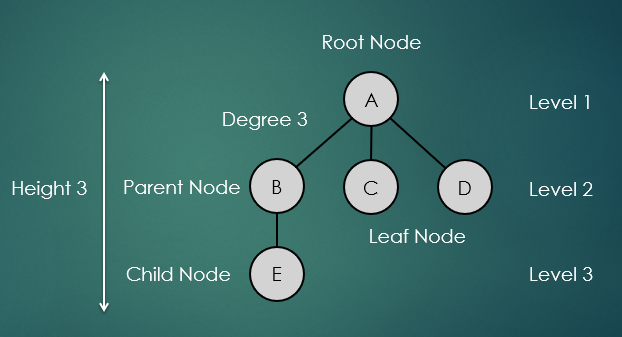
- Root Node : 트리 최상위에 있는 노드
- Child Node : 노드 하위에 연결된 노드
- Degree : 자식노드의 수
- Parent Node : 노드 상위에 연결된 노드
- Leaf Node : 자식이 없는 노드
- Level : Root 노드가 레벨 1에 있고, 아래 층으로 내려가면서 레벨이 1씩 증가
- Height : 트리의 최대 레벨
- Key : 탐색에 사용되는 노드에 저장된 정보
다른 모든 노드는 Root 노드를 통해서 접근이 가능하기 때문에 다른 노드로 가는 경로가 여러가지라면 그것은 Tree 구조가 아니다.
1.3 Binary Search Tree 특성
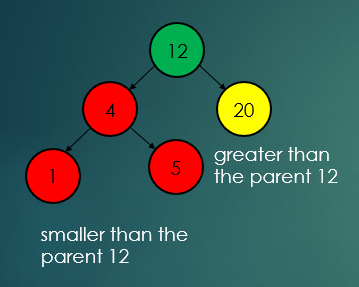
- 모든 노드는 최대 2개의 자식 노드(왼쪽, 오른쪽)를 가질 수 있다.
- 왼쪽 노드는 부모 노드보다 작다
- 오른쪽 노드는 부모 노드보다 크다.
- 키를 정렬된 상태로 유지하기 때문에 조회 및 다른 연산 작업에서 이진 탐색의 원리를 사용할 수 있다.
- 작업량이 트리의 절반을 건너뛰기때문에 조회, 삽입, 삭제는 트리에 저장된 항목 수의 로그와 비례한다.
- 정렬되지 않은 배열에서 키로 항목을 찾는데 필요한 O(N)보다는 낫지만 HashTable보다는 느리다.
2. Binary Search 연산과정
2.1 삽입
삽입 연산은 루트 노드부터 시작한다. 삽입하려는 데이터가 루트 노드의 데이터를 기준으로 크기가 크면 오른쪽, 작으면 왼쪽으로 자식 노드에 위치한다.
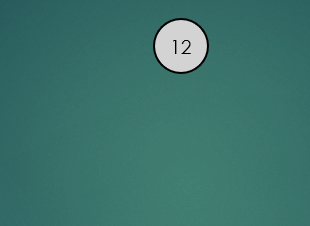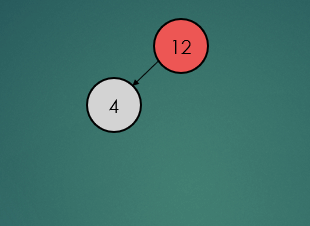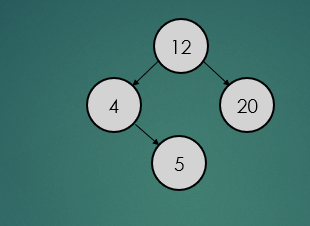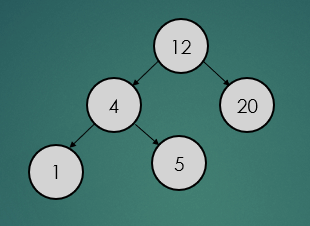
binarySearchTree.insert(12);
binarySearchTree.insert(4);
binarySearchTree.insert(5);
binarySearchTree.insert(20);
binarySearchTree.insert(1);
2.2 탐색
탐색 연산은 탐색하려는 데이터가 루트 노트보다 크면 오른쪽, 작으면 왼쪽 순으로 탐색하려는 데이터를 찾을 때까지 탐색 연산을 수행한다.
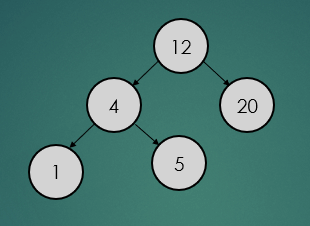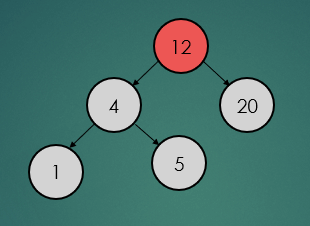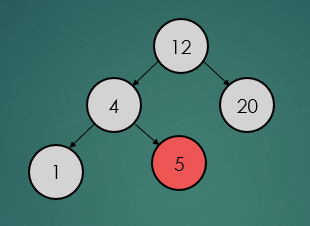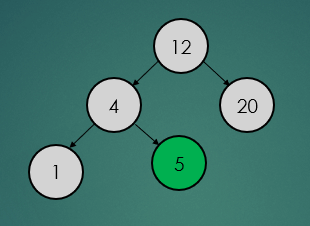
binarySearchTree.find(5);
가장 작은 노드를 찾을 경우에는 최대한 왼쪽으로 이동하면된다.
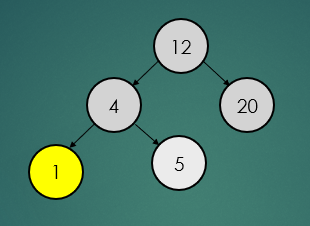
binarySearchTree.find(1);
가장 큰 노드를 찾을 경우에는 최대한 오른쪽으로 이동하면 된다.
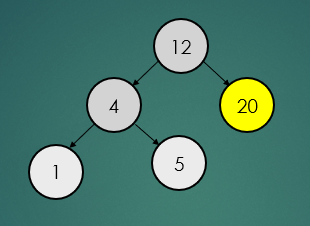
binarySearchTree.find(20);
2.3 삭제
Binary Search Tree의 삭제 연산은 아래와 같이 3개의 경우의 수가 존재한다.
- 삭제할 노드가 leaf 노드인 경우
- 삭제할 노드가 한 개의 자식 노드를 가진 경우
- 삭제할 노드가 두 개의 자식 노드를 가진 경우
2.3.1 : 삭제할 노드가 leaf 노드일 경우
제거할 노드가 leaf 노드일 경우는 아래와 간단하게 제거하기만 하면 된다.
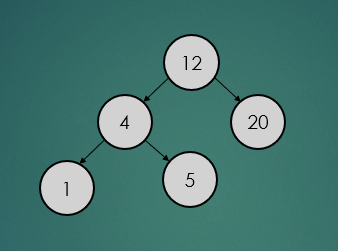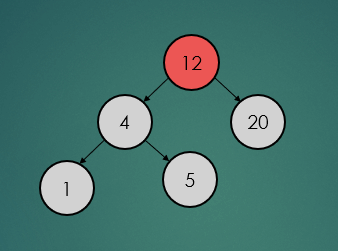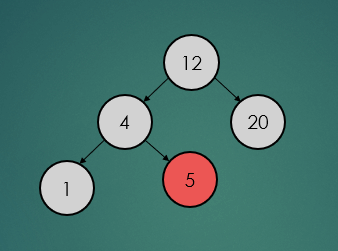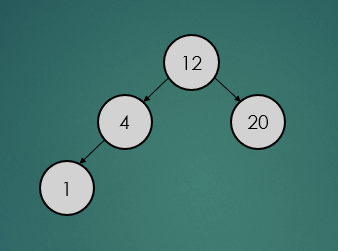
binarySearchTree.remove(5);
2.3.2 : 삭제할 노드가 한 개의 자식노드를 가진 경우
제거할 노드가 하나의 자식 노드를 가진 경우는 아래와 같이 참조값을 변경하기만 하면 된다.
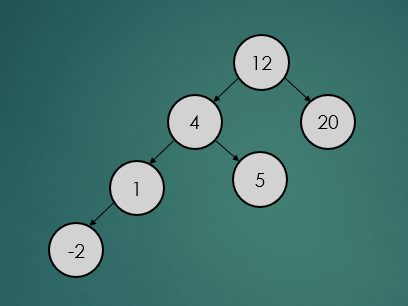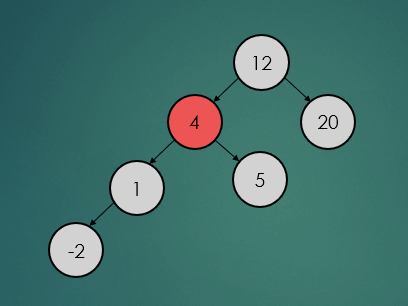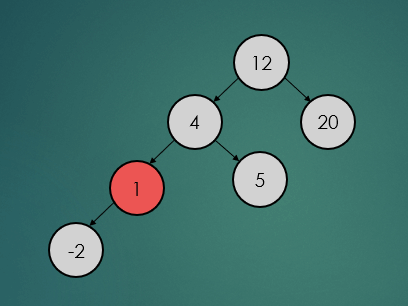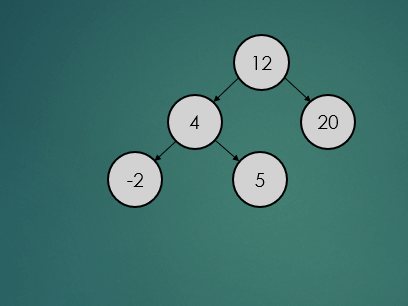
binarySearchTree.remove(1);
2.3.2 : 삭제할 노드가 두 개의 자식노드를 가진 경우
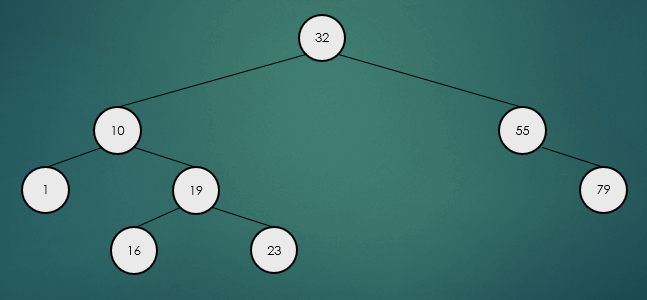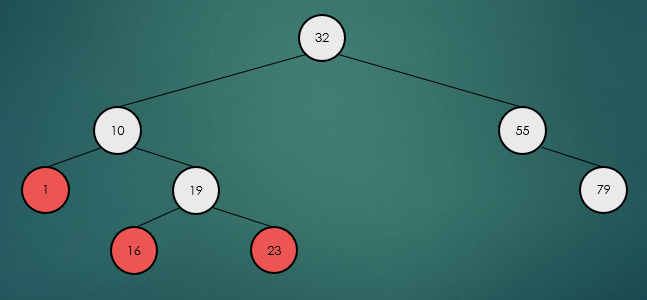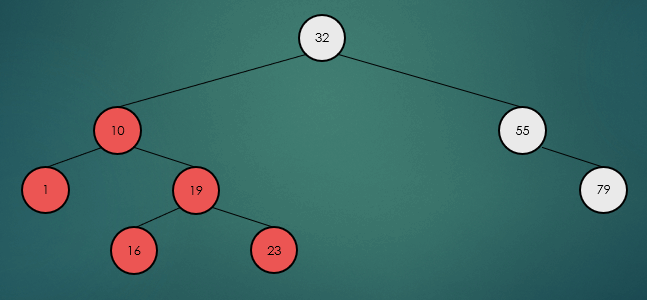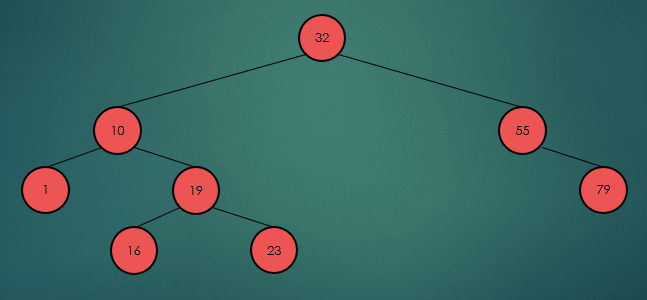
제거할 노드가 2개의 자식 노드를 가진 경우 왼쪽 하위 트리에서 가장 큰 항목 또는 오른쪽 하위 트리에서 가장 작은 항목을 찾아 서로의 위치를 바꾸고, 노드를 제거한다.
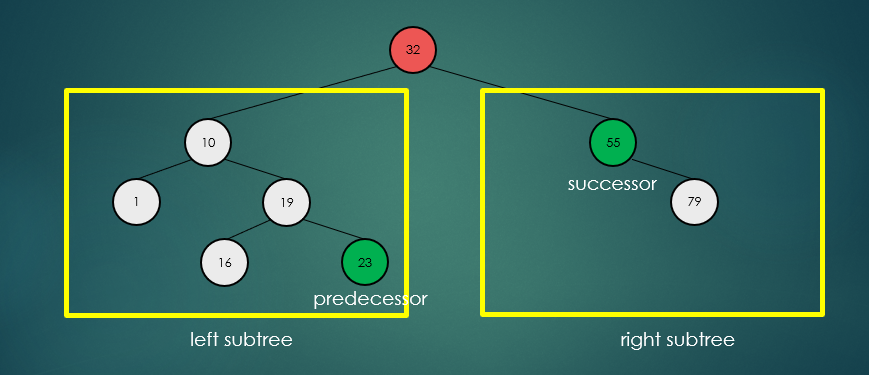
왼쪽 하위 트리에서 가장 큰 항목을 찾아 제거했을 경우
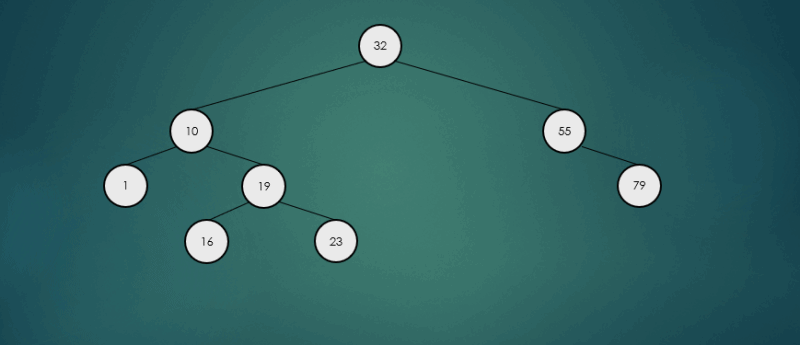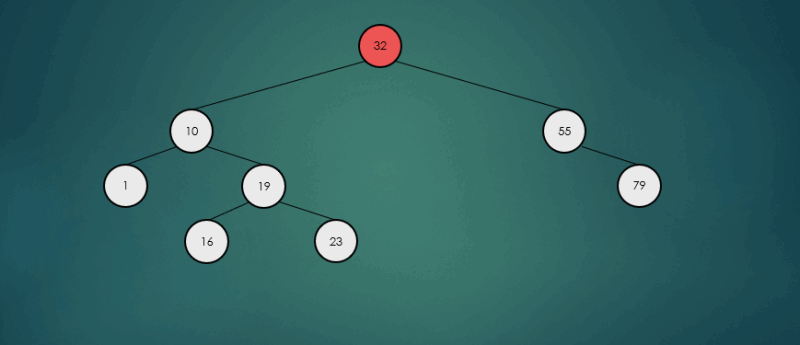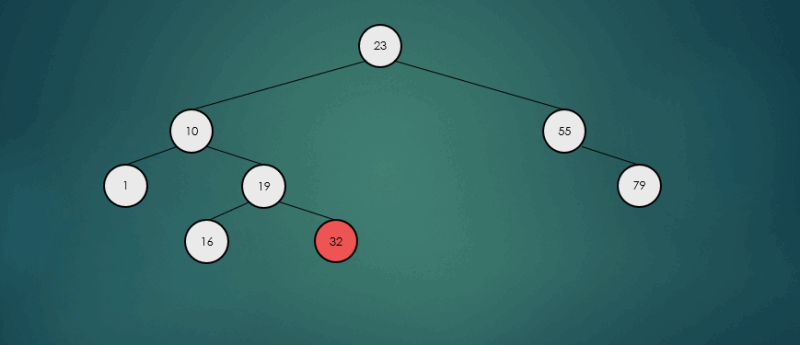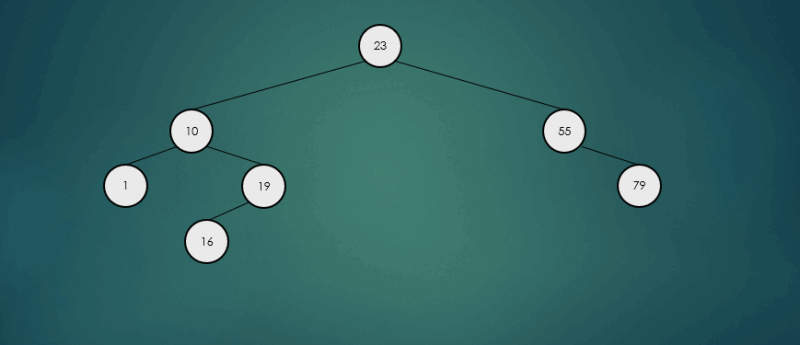
오른쪽 하위 트리에서 가장 큰 항목을 찾아 제거했을 경우
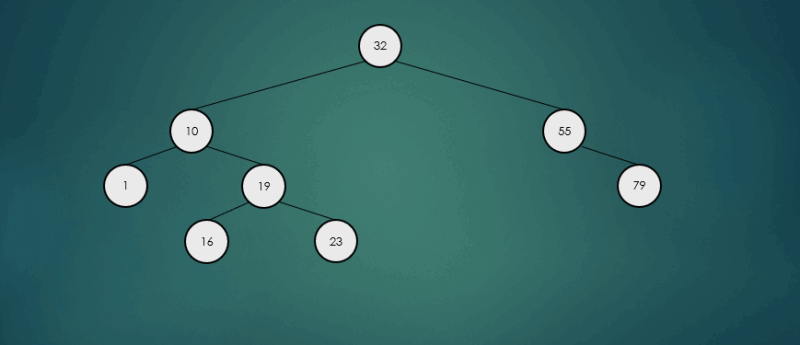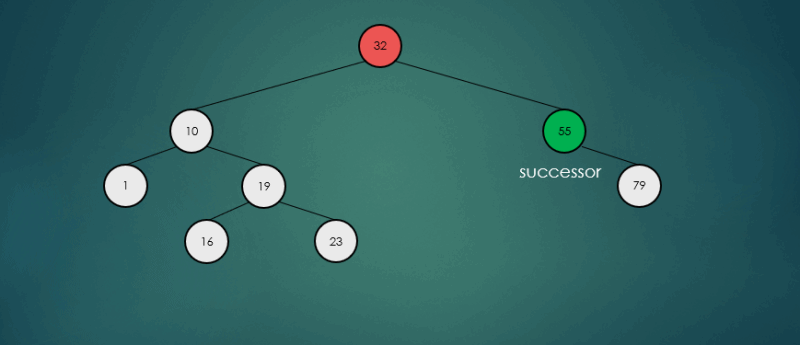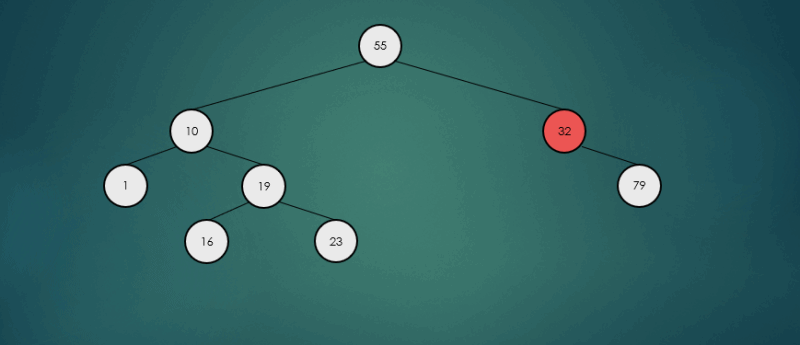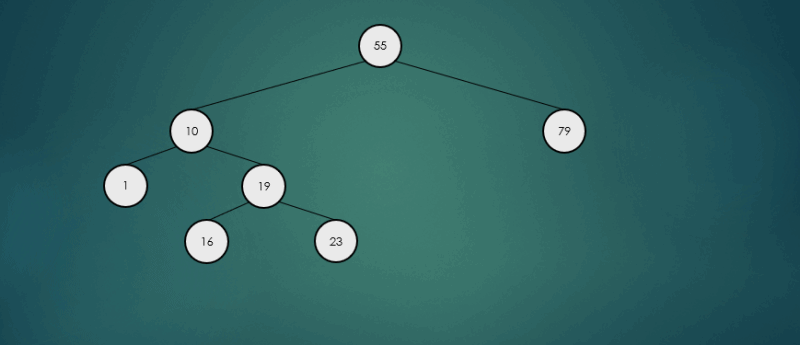
binarySearchTree.remove(32);
2.3 순회
이진탐색트리에서 수행되는 기본 연산들은 트리를 순회하면서 이루어지는데 이진탐색트리의 순회 방식은 다음과 같이 3가지로 나뉜다.
- In-order traversal : 중위 순회
- Pre-order traversal : 전위 순회
- Post-order traversal : 후위 순회
중위 순회는 왼쪽 하위 트리부터 루트 노드, 오른쪽 하위 트리 순으로 반복적으로 방문한다.
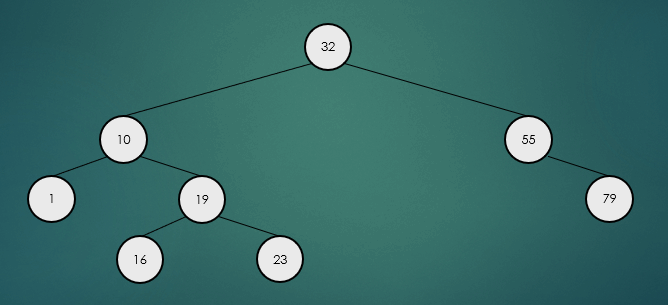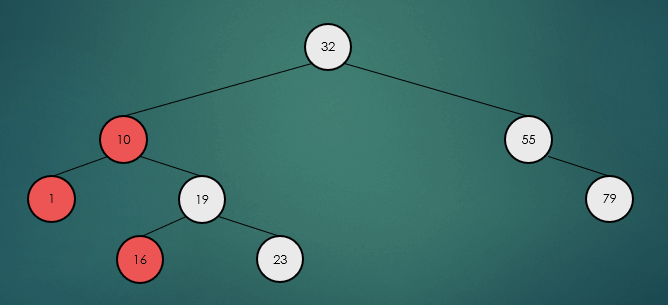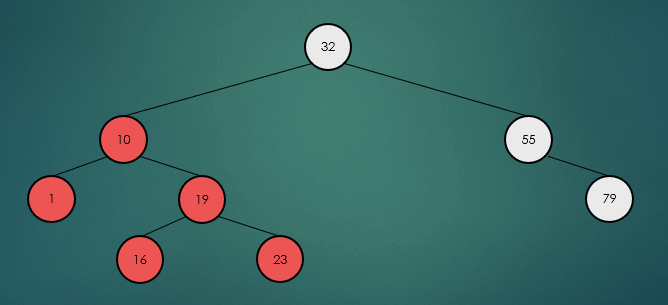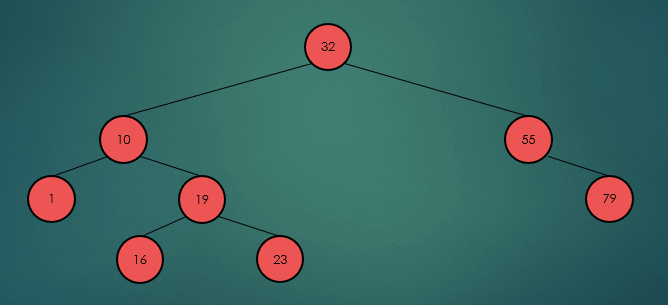
전위 순회는 루트 노드부터 왼쪽 하위 트리, 오른쪽 하위 트리 순으로 반복적으로 방문한다.
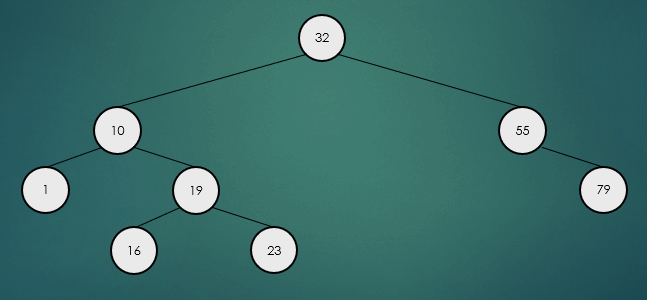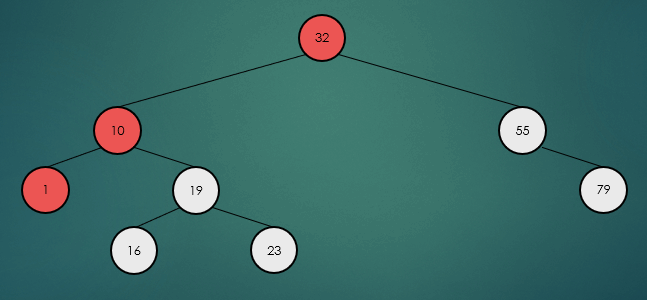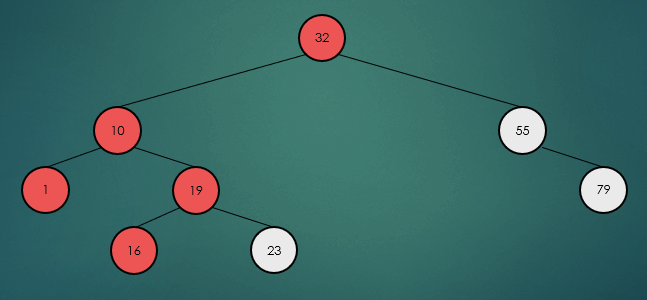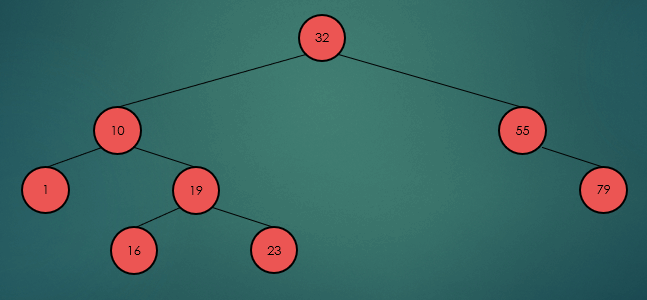
후위 순회는 왼쪽 하위 트리부터 오른쪽 하위트리, 루트 노드 순으로 반복적으로 방문한다.
3. Binary Search Tree 직접 구현 해보기
3.1 클래스 작성
아래와 같이 Node, Tree, BinarySearchTree 클래스와 인터페이스를 작성해준다.
// 노드 클래스
public class Node<T> {
private T data; // 노드 데이터
private Node<T> leftChild; // 왼쪽 하위 노드
private Node<T> rightChild; // 오른쪽 하위 노드
// 생성자
public Node(T data) {
this.data = data;
}
// getter, setter, toString()
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
public Node<T> getLeftChild() {
return leftChild;
}
public void setLeftChild(Node<T> leftChild) {
this.leftChild = leftChild;
}
public Node<T> getRightChild() {
return rightChild;
}
public void setRightChild(Node<T> rightChild) {
this.rightChild = rightChild;
}
@Override
public String toString() {
return this.data.toString();
}
}
// 트리 인터페이스
public interface Tree<T> {
public void insert(T data); // 삽입
public T getMinValue(); // 최소값
public T getMaxValue(); // 최대값
public void traversal(); // 순회
public void delete(T data); // 삭제
}
// 이진 탐색 트리 클래스
public class BinarySearchTree<T extends Comparable<T>> implements Tree<T> {
private Node<T> root; // 루트 노드
// 삽입
@Override
public void insert(T data) {
}
// 최소값 반환
@Override
public T getMinValue() {
return null;
}
// 최대값 반환
@Override
public T getMaxValue() {
return null;
}
// 순회 : 중위, 전위, 후위
@Override
public void traversal() {
}
// 삭제
@Override
public void delete(T data) {
}
}
3.2 삽입
삽입 연산은 아래와 같다.
// 삽입
@Override
public void insert(T data) {
// 루트노드가 null 이면 루트 노드 삽입
if (root == null) {
root = new Node<>(data);
// 아니면 하위노드에 삽입
} else {
insertNode(data, root);
}
}
// 삽입
private void insertNode(T newData, Node<T> node) {
// 새로운 데이터가 기존의 데이터보다 작으면 : 왼쪽 하위노드
if (newData.compareTo(node.getData()) < 0) {
// 왼쪽 하위노드가 존재하면 하위노드에 삽입하기 위해 재귀호출
if (node.getLeftChild() != null) {
insertNode(newData, node.getLeftChild());
// 왼쪽 하위노드가 없다면 노드를 생성, 상위노드의 왼쪽 하위노드에 설정
} else {
Node<T> newNode = new Node<>(newData);
node.setLeftChild(newNode);
}
// 새로운 데이터가 기존의 데이터보다 크거나 같으면 : 오른쪽 하위노드
} else {
// 오른쪽 하위 노드가 존재하면 하위 노드에 삽입하기 위해 재귀호출
if (node.getRightChild() != null) {
insertNode(newData, node.getRightChild());
// 오른쪽 하위 노드가 없다면 노드를 생성, 상위노드의 오른쪽 하위 노드에 설정
} else {
Node<T> newNode = new Node<>(newData);
node.setRightChild(newNode);
}
}
}
3.3 최소 / 최대 값 반환
// 최소값 반환
@Override
public T getMinValue() {
if (root == null) {
return null;
}
return getMin(root);
}
// 최대값 반환
@Override
public T getMaxValue() {
if (root == null) {
return null;
}
return getMax(root);
}
// 최소값 : 가장 왼쪽에 위치한 노드가 최소값을 가지고 있다.
private T getMin(Node<T> node) {
// 가장 왼쪽에 위치한 노드를 찾을 때까지 재귀호출
if (node.getLeftChild() != null) {
return getMin(node.getLeftChild());
}
return node.getData();
}
// 최대값 : 가장 오른쪽에 위치한 노드가 최대값을 가지고 있다.
private T getMax(Node<T> node) {
// 가장 오른쪽에 위치한 노드를 찾을 때까지 재취호출
if (node.getRightChild() != null) {
return getMax(node.getRightChild());
}
return node.getData();
}
3.4 순회
// 순회 : 중위, 전위, 후위
@Override
public void traversal() {
if (root != null) {
inOrderTraversal(root);
System.out.println();
preOrderTraversal(root);
System.out.println();
postOrderTraversal(root);
System.out.println();
}
}
// 중위 순회
private void inOrderTraversal(Node<T> node) {
if (node.getLeftChild() != null) {
inOrderTraversal(node.getLeftChild());
}
System.out.print(node + " --> ");
if (node.getRightChild() != null) {
inOrderTraversal(node.getRightChild());
}
}
// 전위 순회
private void preOrderTraversal(Node<T> node) {
System.out.print(node + " --> ");
if (node.getLeftChild() != null) {
preOrderTraversal(node.getLeftChild());
}
if (node.getRightChild() != null) {
preOrderTraversal(node.getRightChild());
}
}
// 후위 순회
private void postOrderTraversal(Node<T> node) {
if (node.getLeftChild() != null) {
preOrderTraversal(node.getLeftChild());
}
if (node.getRightChild() != null) {
preOrderTraversal(node.getRightChild());
}
System.out.print(node + " --> ");
}
3.5 삭제
// 삭제
@Override
public void delete(T data) {
if (root != null) {
root = delete(root, data);
}
}
// 삭제
private Node<T> delete(Node<T> node, T data) {
if (node == null) {
return node;
}
// 삭제할 데이터가 현재 노드의 데이터보다 작으면 왼쪽 하위노드 탐색
if (data.compareTo(node.getData()) < 0) {
// 삭제 재귀 호출
node.setLeftChild(delete(node.getLeftChild(), data));
// 삭제할 데이터가 현재 노드의 데이터보다 크면 오른쪽 하위노드 탐색
} else if (data.compareTo(node.getData()) > 0) {
// 삭제 재귀 호출
node.setRightChild(delete(node.getRightChild(), data));
// 삭제할 데이터가 현재 노드의 데이터와 같으면 삭제
} else {
// 하위 노드가 없는 leaf 노드이면
if (node.getLeftChild() == null && node.getRightChild()== null) {
System.out.println("removing a leaf node...");
return null;
}
// 왼쪽 하위노드가 null 이면 : 오른쪽 하위 노드만 있다면
if (node.getLeftChild() == null) {
System.out.println("removing the right child...");
Node<T> tempNode = node.getRightChild();
node = null;
return tempNode;
// 오른쪽 하위노드가 null 이면 : 왼쪽 하위 노드만 있다면
} else if (node.getRightChild() == null) {
System.out.println("removing the left child...");
Node<T> tempNode = node.getLeftChild();
node = null;
return tempNode;
}
// 하위노드가 2개인 경우
System.out.println("removing item with two children...");
// 왼쪽의 하위 노드중에서 가장 큰 노드 탐색
Node<T> tempNode = getPredecessor(node.getLeftChild());
// 삭제하려는 노드와 왼쪽 하위노드에서 가장 큰 노드와 swap
node.setData(tempNode.getData());
// 삭제 재귀 호출
node.setLeftChild(delete(node.getLeftChild(), tempNode.getData()));
}
return node;
}
// 왼쪽 하위노드에서 가장 큰 노드 탐색
private Node<T> getPredecessor(Node<T> node) {
if (node.getRightChild() != null) {
return getPredecessor(node.getRightChild());
}
System.out.println("Predecessor : " + node);
return node;
}
3.6 객체 사용을 위한 클래스 작성
// 사람 클래스
public class Person implements Comparable<Person> {
private String name;
private int age;
public Person(String name, int age) {
this.name = name;
this.age = age;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
@Override
public String toString() {
return this.name + " : " + this.age;
}
@Override
public int compareTo(Person person) {
return this.name.compareTo(person.getName());
}
}
3.7 테스트
// 테스트 클래스
public class App {
public static void main(String[] args) {
Tree<Integer> bst = new BinarySearchTree<>();
bst.insert(41);
bst.insert(20);
bst.insert(11);
bst.insert(29);
bst.insert(32);
bst.insert(65);
bst.insert(50);
bst.insert(91);
bst.insert(72);
bst.insert(99);
bst.traversal();
bst.delete(41);
bst.traversal();
System.out.println("=============================");
System.out.println(bst.getMinValue());
System.out.println(bst.getMaxValue());
System.out.println("=============================");
Tree<Person> bst2 = new BinarySearchTree<>();
bst2.insert(new Person("Kim" , 23));
bst2.insert(new Person("Lee" , 25));
bst2.insert(new Person("Park" , 28));
bst2.insert(new Person("Choi" , 29));
bst2.insert(new Person("Yoon" , 32));
bst2.insert(new Person("Lim" , 21));
bst2.insert(new Person("Ahn" , 33));
bst2.traversal();
}
}
// 실행 결과
11 --> 20 --> 29 --> 32 --> 41 --> 50 --> 65 --> 72 --> 91 --> 99 -->
41 --> 20 --> 11 --> 29 --> 32 --> 65 --> 50 --> 91 --> 72 --> 99 -->
20 --> 11 --> 29 --> 32 --> 65 --> 50 --> 91 --> 72 --> 99 --> 41 -->
removing item with two children...
Predecessor : 32
removing a leaf node...
11 --> 20 --> 29 --> 32 --> 50 --> 65 --> 72 --> 91 --> 99 -->
32 --> 20 --> 11 --> 29 --> 65 --> 50 --> 91 --> 72 --> 99 -->
20 --> 11 --> 29 --> 65 --> 50 --> 91 --> 72 --> 99 --> 32 -->
=============================
11
99
=============================
Ahn : 33 --> Choi : 29 --> Kim : 23 --> Lee : 25 --> Lim : 21 --> Park : 28 --> Yoon : 32 -->
Kim : 23 --> Choi : 29 --> Ahn : 33 --> Lee : 25 --> Park : 28 --> Lim : 21 --> Yoon : 32 -->
Choi : 29 --> Ahn : 33 --> Lee : 25 --> Park : 28 --> Lim : 21 --> Yoon : 32 --> Kim : 23 -->
4. Binary Search Tree 문제해결
4.1 Compare binary Search trees : 이진 탐색 트리 비교하기
- Write an efficient algorithm that’s able to compare two binary search trees.
- The method returns true if the trees are identical (same topology with same values in the nodes) otherwise it returns false.
이진 탐색 트리 간의 구조와 값에 관해 일치하는지 비교하는 코드를 작성해보자. 하지만 문제는 아래와 같이 모든 노드들이 동일한 값을 가지지만 구조는 동일하지 않을 경우가 있다.
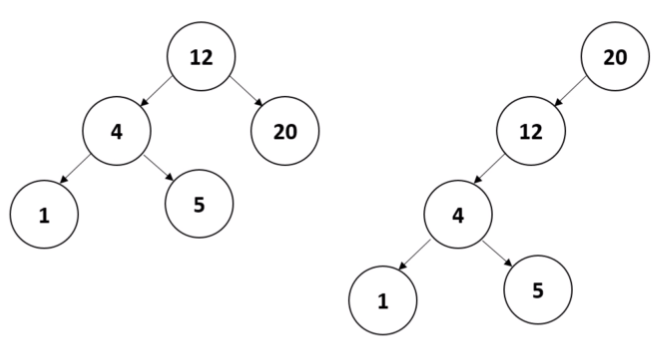
이 문제를 해결하기 위해 두 개의 이진 탐색 트리를 동시에 전위 순회를 하면서 값을 비교하는 방식으로 처리해보자.
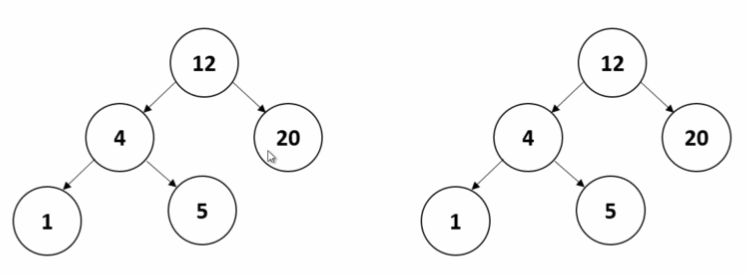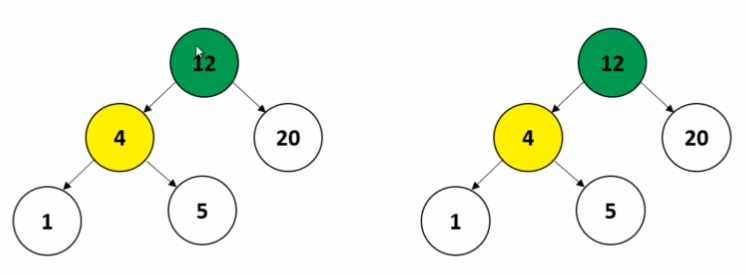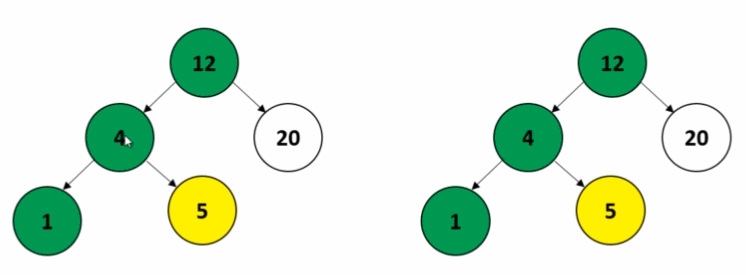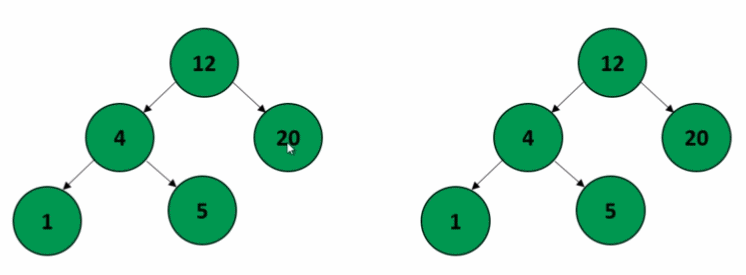
위에서 작성한 이진 탐색 트리의 코드에서 루트 노드를 반환하는 메서드를 추가해준다.
// Tree 인터페이스
public Node<T> getRoot(); // 루트노드 반환
// Binary Search Tree 클래스
// 루트 노드 반환
@Override
public Node<T> getRoot() {
return this.root;
}
그리고 이진 탐색 트리를 비교하는 helper 클래스를 아래와 같이 작성해준다.
// 이진탐색트리를 비교하는 helper 클래스
public class TreeCompareHelper<T extends Comparable<T>> {
public boolean compareTrees(Node<T> node1, Node<T> node2) {
// 두 노드가 leaf 노드인지 체크
if (node1 == null || node2 == null) {
return node1 == node2;
}
// 노드간의 데이터 비교
if (node1.getData().compareTo(node2.getData()) != 0) {
return false;
}
// 왼쪽 하위트리와 오른쪽 하위트리의 값들이 일치하는지 확인하기 위해 재귀호출
return compareTrees(node1.getLeftChild(), node2.getLeftChild()) && compareTrees(node1.getRightChild(), node2.getRightChild());
}
}
첫번째 조건문은 경우 이진탐색트리의 구조가 같은지 확인 하기위해 아래와 같이 두 노드가 leaf 노드인지를 확인한다.
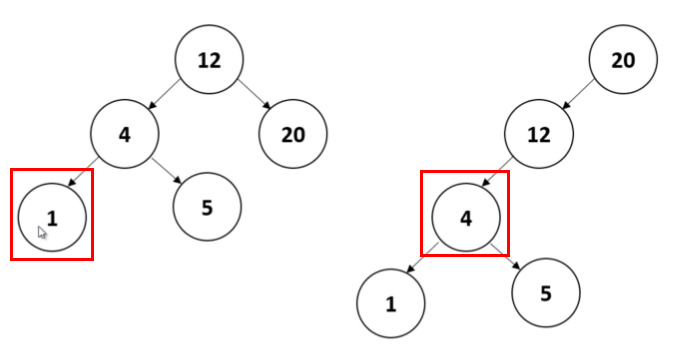
두번째 조건문은 아래와 같이 두 노드가 가진 데이터의 값이 일치하는지 확인한다.
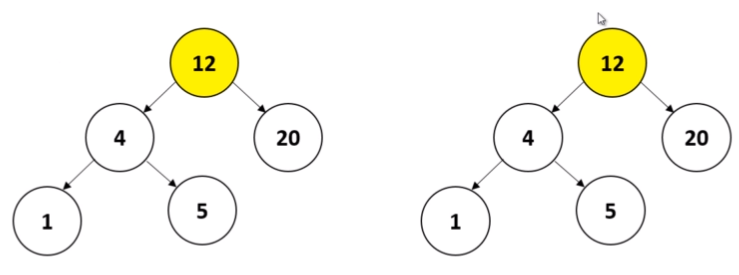
마지막으로 이진 탐색 트리의 왼쪽 하위 트리와 오른쪽 하위트리의 값들이 일치하는지
확인하기 위해 AND 연사자를 사용해 각각 compareTrees()메서드를 재귀호출 수행한다.
compareTrees(node1.getLeftChild(), node2.getLeftChild()) && compareTrees(node1.getRightChild(), node2.getRightChild());
// 테스트 클래스
public class App {
public static void main(String[] args) {
Tree<Integer> bst1 = new BinarySearchTree<>();
bst1.insert(2);
bst1.insert(55);
bst1.insert(67);
bst1.insert(12);
bst1.insert(11);
Tree<Integer> bst2 = new BinarySearchTree<>();
bst2.insert(2);
bst2.insert(55);
bst2.insert(67);
bst2.insert(12);
bst2.insert(11);
Tree<Integer> bst3 = new BinarySearchTree<>();
bst3.insert(2);
bst3.insert(50);
bst3.insert(67);
bst3.insert(12);
bst3.insert(11);
TreeCompareHelper<Integer> helper = new TreeCompareHelper<>();
System.out.println(helper.compareTrees(bst1.getRoot(), bst2.getRoot()));
System.out.println(helper.compareTrees(bst1.getRoot(), bst3.getRoot()));
}
}
위와 같이 코드를 작성하고 실행결과를 확인하면 아래와 같이 일치하는지 일치하지 않는지 알 수 있다.
// 실행결과
true
false
4.2 k-th smallest element in a search tree : 이진 탐색트리에서 K번째로 작은 요소 찾기
- Write an efficient in-place algorithm to find the k-th smallest (largest) item in a binary search tree!
이진 탐색 트리에서 k 번째로 작은 요소를 찾는 방법에 대해 알아보자.
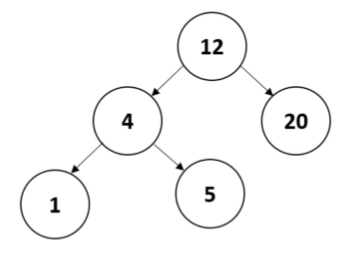
주어진 노드 T 의 왼쪽 하위 트리에는 T 보다 작은 요소가 포함된다.
- K 가 왼쪽 하위 트리의 노드 수보다 작은 경우 K 번째로 작은 항목은 왼쪽 하위 트리에 있어야만 한다.
- K 가 왼쪽 하위 트리의 노드 수보다 크다면 오른쪽 하위 트리를 확인해야한다.
2번째로 작은 요소를 찾는 과정을 정리해보자.
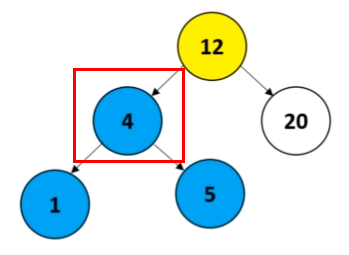
- 가장 먼저 왼쪽 하위 트리의 노드들을 확인한다.
- 왼쪽 하위 트리에는 3개의 노드가 있기 때문에 노드의 수는 K 값보다 크다.
- 그러므로 2번째로 작은 요소는 왼쪽 하위 트리에 존재한다.
- 2번째로 작은 요소를 찾기 위해 왼쪽 하위 트리에서 재귀호출을 수행한다.
4번째로 작은 요소를 찾는 과정을 정리해보자.
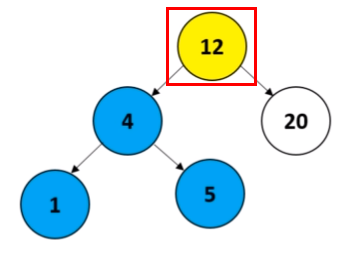
- 가장 먼저 왼쪽 하위 트리의 노드들을 확인한다.
- 왼쪽 하위 트리에 있는 노드의 수에 1을 더한 값이 K 라면 루트 노드이다.
5번째로 작은 요소를 찾는 과정을 정리해보자.
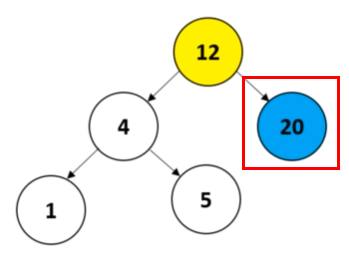
- 가장 먼저 왼쪽 하위 트리의 노드들을 확인한다.
- 왼쪽 하위 트리의 노드들과 루트 노드의 합이 K 의 값보다 작다.
- 그러므로 오른쪽 하위 트리를 확인해야하는데 K 의 값이 변경되어야 한다.
- K - (왼쪽 노드의 수 + 루트노드) 의 계산을 통해 K 값이 변경된다.
그렇다면 위의 내용을 정리해 알고리즘으로 표현해보자.
int n = number of nodes in the left subtree + 1
if(n == k) return node;
if(n > k) return kthSmallest(leftSubtree, k)
if(n < k) return kthSmallest(rightSubtree, k-n)
위의 알고리즘을 바탕으로 실제 코드로 구현하면 아래와 같다.
// Tree 인터페이스
public Node<T> getKthSmallest(Node<T> node, int k); // k번째 작은 요소 찾기
// Binary Search Tree 클래스
// K번째 작은 요소 반환
@Override
public Node<T> getKthSmallest(Node<T> node, int k) {
// 왼쪽 하위 트리의 갯수 + 루트 노드
int n = treeSize(node.getLeftChild()) + 1;
// 가장 작은 요소를 찾을 경우
if (n == k) {
return node;
}
// 찾는 요소가 왼쪽 하위 트리에 존재할 경우
if (n > k) {
return getKthSmallest(node.getLeftChild(), k);
}
// 찾는 요소가 오른쪽 하위 트리에 존재할 경우
return getKthSmallest(node.getRightChild(), k - n);
}
// 트리 사이즈 반환
private int treeSize(Node<T> node) {
if (node == null) {
return 0;
}
// 왼쪽 하위 트리 + 오른쪽 하위 트리의 사이즈를 구하기 위해 재귀호출
// 트리의 사이즈 = 왼쪽 하위 트리 사이즈 + 오른쪽 하위 트리 사이즈 + 1
return (treeSize(node.getLeftChild()) + treeSize(node.getRightChild()) + 1);
}
위에서 구현한 코드가 제대로 작동하는지 확인해보자.
public class App {
public static void main(String[] args) {
Tree<Integer> bst = new BinarySearchTree<>();
bst.insert(2);
bst.insert(55);
bst.insert(67);
bst.insert(12);
bst.insert(11);
System.out.println(bst.getKthSmallest(bst.getRoot(), 4));
}
}
// 결과 확인
55