본 글은 Udemy의 자바 자료구조 강의를 듣고 개인적으로 학습한 내용 복습하기 위해 작성된 글로 내용상 오류가 있을 수 있습니다. 오류가 있다면 지적 부탁 드리겠습니다.
1. AVL Tree란?
AVL트리는 트리가 한쪽으로 치우쳐 자라나는 현상을 방지하여 트리 높이의 균형을 유지하는 이진탐색트리이다. Balanced 이진탐색트리를 만들면 N개의 노드를 가진 트리의 높이가 O(logN)이 되어 탐색, 삽입, 삭제 연산의 수행시간이 O(logN)이 보장된다.
1.1 Linked List, Binary Search Tree, Balanced Binary Tree 비교
AVL 트리에 대해 알아보기 전에 3가지 자료구조의 차이점에 대해 알아보자.
- Linked List
- 구현이 쉬움
- 많은 포인터(참조)를 저장
- O(N) 시간복잡도를 가짐
- Binary Search Tree
- 탐색의 O(N) 시간복잡도를 O(logN) 시간복잡도로 줄임
- Unbalanced Tree일 경우 탐색의 속도는 느려짐
- Balanced Binary Tree(AVL Tree, Red-Black Tree)
- 균형을 이루도록 보장
- 항상 O(logN)의 시간복잡도를 보장
예를 들어 이진탐색트리에 정렬된 배열[1, 2, 3, 4]를 차례로 저장한다고 가정하면 아래와 같다.
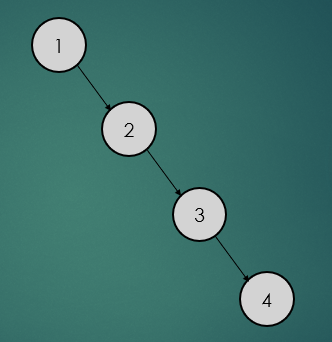
이렇게 이진탐색트리에 정렬된 배열을 저장하면, 결국 연결리스트가 되고, 시간복잡도는 O(logN)이 아닌 O(N)이 된다.
1.2 AVL Tree의 특성
- 이진탐색트리 연산 실행시간은 이진탐색트리의 높이에 따라 달라지는데 최상의 성능을 얻으려면 트리의 균형을 유지해야한다.
- AVL 트리에서 노드의 두 하위 트리(왼쪽, 오른쪽)의 높이의 차이가 최대 1을 넘지 않는다.
- AVL 트리는 엄격하게 균형을 유지하기 때문에 Red-black 트리보다 더 빠른 성능을 가지지만 더 많은 작업을 수행해야만 한다.
- 특히 운영체제의 경우 이러한 자료구조에 의존한다.
- 대부분의 연산은 이진탐색트리와 동일하다.
- 이진탐색트리와 동일하게 모든 노드는 최대 2개의 자식노드를 가질수 있고, 왼쪽 자식노드는 부모 노드보다 작고, 오른쪽 자식노드는 크다.
- 삽입 연산의 경우 이진탐색트리와 동일하지만 모든 삽입연산은 트리가 균형을 유지하는지 확인을 해야한다.
- 삭제, 최대/최소값 반환 연산 또한 마찬가지이다.
2. AVL Tree 연산과정
2.1 연산의 시간복잡도(Time Complexity)
AVL 트리의 기본연산은 이진탐색트리와 동일하지만 아래의 표를 보면 시간복잡도가 다르다.
| 이진탐색트리 | 평균 | 최악 |
|---|---|---|
| 공간 | O(N) | O(N) |
| 삽입 | O(logN) | O(N) |
| 삭제 | O(logN) | O(N) |
| 탐색 | O(logN) | O(N) |
| AVL트리 | 평균 | 최악 |
|---|---|---|
| 공간 | O(N) | O(N) |
| 삽입 | O(logN) | O(logN) |
| 삭제 | O(logN) | O(logN) |
| 탐색 | O(logN) | O(logN) |
2.2 탐색(Search)
AVL 트리의 탐색은 이진트리와 동일하다.
2.2.1 특정 노드 탐색
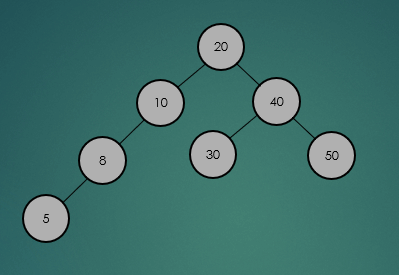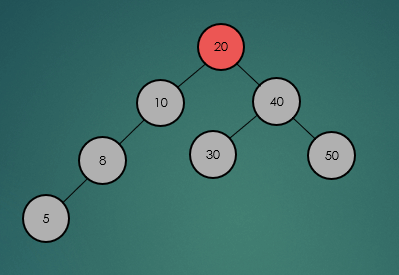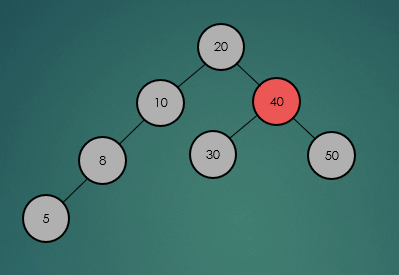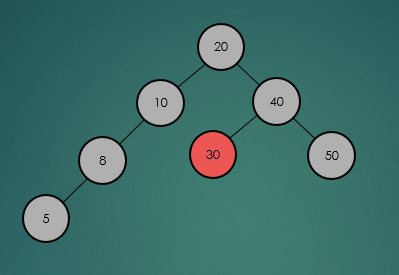
2.2.2 최소, 최대값 탐색
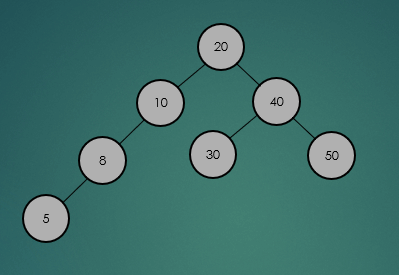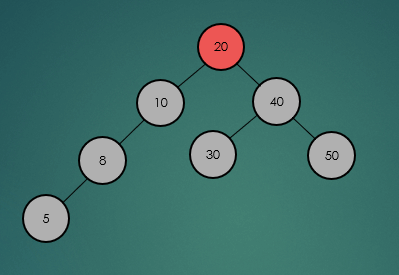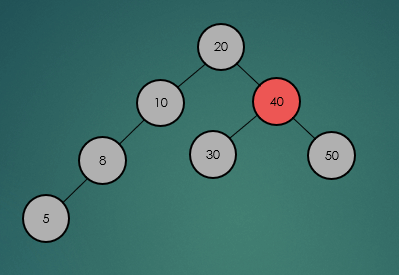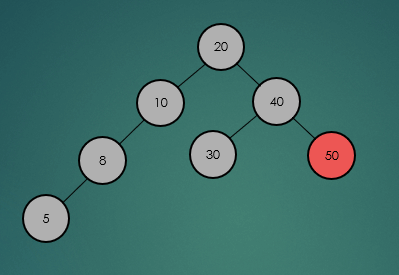
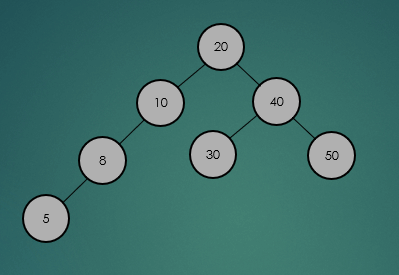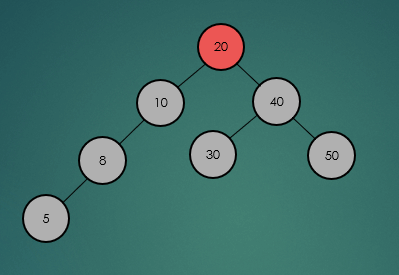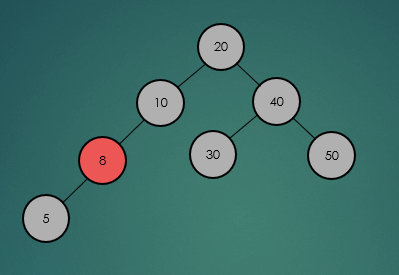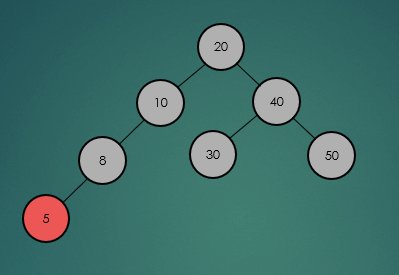
2.3 높이(Height)
AVL 트리의 연산을 수행하고, 불균형이 발생하면 회전을 통해 균형을 다시 맞춘다. 이렇게 균형을 맞추기 위해서는 각 노드들의 높이를 알아야만 한다. 그렇기 때문에 각 노드의 높이를 계산하는 과정을 이해하는 것이 중요하다.
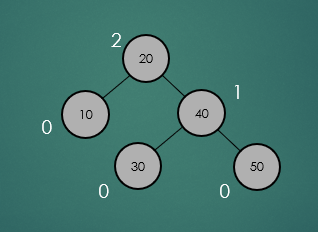
노드의 높이는 특정 노드부터 leaf 노드까지 가장 긴 경로의 길이를 말한다.
height = max(leftChild.height(), rightChild.height()) + 1
특정 노드의 높이를 계산하는 방법은 위와 같은 코드를 통해 계산을 할 수 있다.
- 특정노드의 왼쪽, 오른쪽 자식노드의 높이 중에서 가장 큰 값을 1을 더한 값이 특정 노드의 높이가 된다.
- leaf 노드는 null인 자식노드를 가지고 있는데 이런 경우 자식 노드의 높이는 -1로 간주한다.
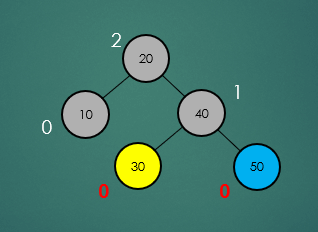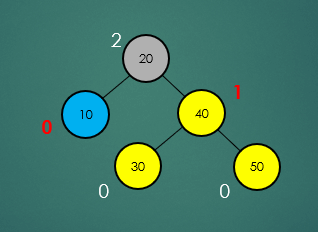
- 위의 그림을 보면 AVL 트리는 모든 노드의 왼쪽, 오른쪽 자식노드의 높이가 최대 +1, 최소 -1의 차이만을 허용한다는 것을 알 수 있다.
2.4 회전(Rotation)
AVL 트리에서 삽입, 삭제 연산을 수행할 때 트리의 균형을 유지하기 위해 LL-회전, RR-회전, LR-회전, RL-회전연산이 사용된다. 각 회전연산은 두 종류의 기본적인 연산으로 구현된다.
rightRotate(): 오른쪽 방향으로 회전leftRotate(): 왼쪽 방향으로 회전
rightRotate()은 왼쪽 방향의 서브트리가 높아서 불균형이 발생할 때 서브트리를
오른쪽 방향으로 회전하기 위한 메서드이고, leftRotate()는 오른쪽 방향의 서브트리가
높아서 불균형이 발생했을 때 왼쪽 방향으로 회전하기 위한 메서드이다.


위의 그림을 보면 오른쪽 또는 왼쪽 회전을 하더라도 중위 순회를 하면 노드를 순회하는 순서는 항상 같다. 즉, 회전을 통해 트리 구조의 불균형을 맞추는 작업만을 수행하는 것이다.
이제 구체적인 상황들을 통해 어떻게 회전을 수행하는지 알아보자.
그전에 앞서 노드의 높이를 통해 불균형상태인지 아닌지를 알아보는 계산식은 아래와 같다. 왼쪽, 오른쪽 하위트리의 높이 차이기 절대 값 1을 초과한 경우 불균형 상태이다.
| height(leftSubtree) - height(rightSubtree) | ≤ 1
2.4.1 Case 1 : 왼쪽으로 트리가 치우친 경우 - LL
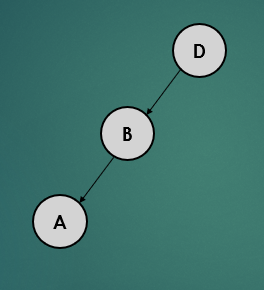
위 트리는 왼쪽으로 치우친 상태인데 이 트리가 어떤 과정을 거쳐 균형 상태로 바뀌는지 살펴보자.
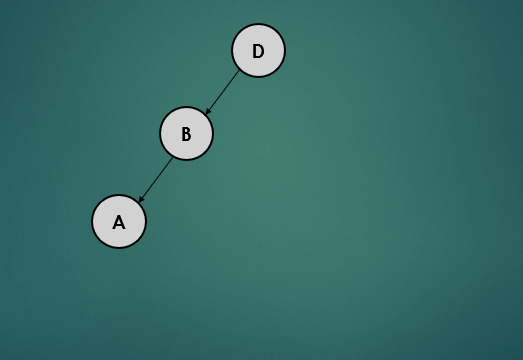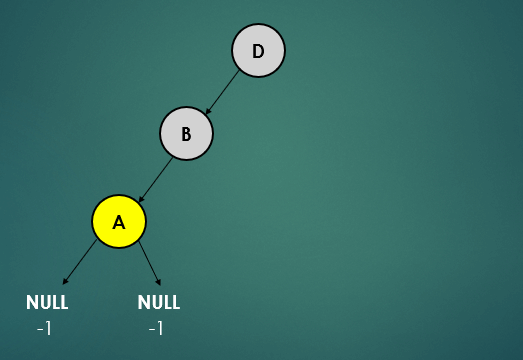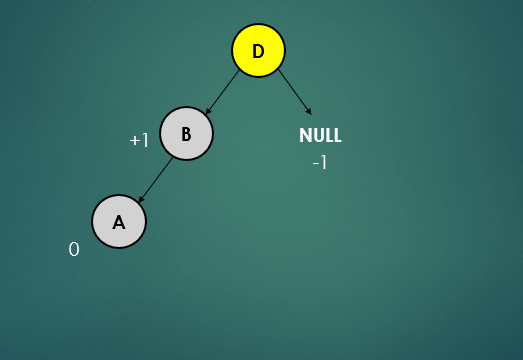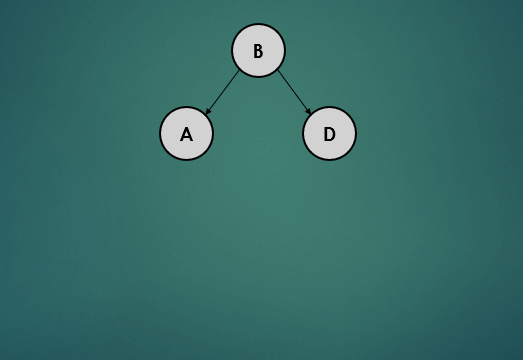
- leaf 노드(A)는 자식노드가 없기 때문에 왼쪽, 오른쪽 자식노드를 -1로 간주하여 높이를 계산하면 0이고 균형상태이다.
- 그 다음 노드인 B는 왼쪽 노드는 0, 오른쪽 노드는 null이기떄문에 -1로 높이를 계산하면 1이고 균형상태이다.
- 루트 노드인 D는 왼쪽노드는 1, 오른쪽 노드는 null이기 때문에 -1로 높이를 계산하면 2이고 하위트리의 높이 차이가 1을 초과하기 때문에 불균형 상태이다.
- 왼쪽으로 치우친 트리의 균형을 잡기 위해 오른쪽으로 회전을 수행한다.
오른쪽으로 회전을 수행하는 알고리즘은 아래와 같다.
BEGIN rotateRight(Node node)
Node tempLeftNode = node.getLeftNode(); // 상위 노드의 왼쪽 하위 노드
Node t = tempLeftNode.getRightNode(); // 왼쪽 하위 노드의 오른쪽 하위 노드
tempLeftNode.setRightNode(node); // 왼쪽 하위 노드의 오른쪽 하위 노드를 상위 노드로 변경
node.setLeftNode(t); // 상위 노드의 왼쪽 노드를 오른쪽 하위 노드로 변경
node.updateHeight(); // 상위 노드의 높이 변경
tempLeftNode.updateHeight(); // 왼쪽 하위 노드 높이 변경
END
2.4.2 Case 2 : 오른쪽으로 트리가 치우친 경우 - RR
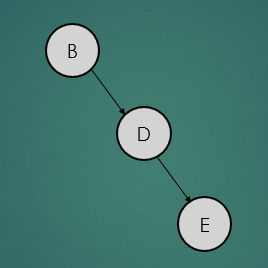
위 트리는 오른쪽으로 트리가 치우친 상태인데 이 트리가 어떤 과정을 거쳐 균형 상태로 바뀌는지 살펴보자.
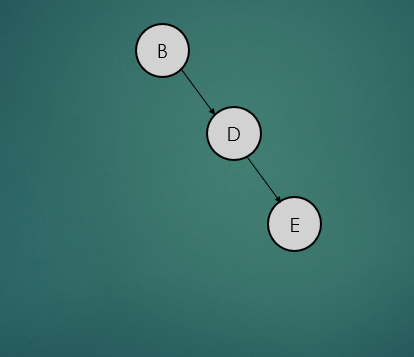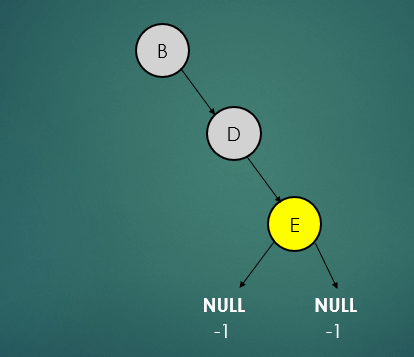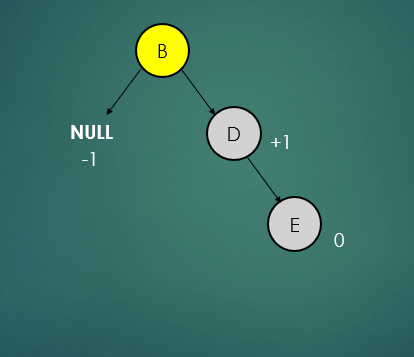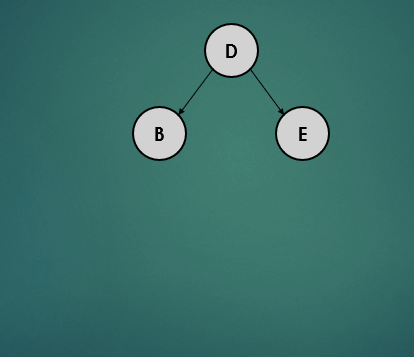
- leaf 노드(E)는 자식노드가 없기 때문에 왼쪽, 오른쪽 자식노드는 -1로 간주하여 높이를 계산하면 0이고 균형상태이다.
- 그 다음 노드인 D는 왼쪽 노드는 null이기때문에 -1, 오른쪽 노드는 0이기떄문에 높이를 계산하면 1이고 균형상태이다.
- 루트 노드인 F는 왼쪽노드는 null이기 때문에 -1, 오른쪽 노드는 1로 높이를 계산하면 2이고 하위트리의 높이 차이가 1을 초과하기 때문에 불균형 상태이다.
- 오른쪽으로 치우친 트리의 균형을 잡기 위해 왼쪽으로 회전을 수행한다.
왼쪽으로 회전할 때의 알고리즘은 아래와 같다.
BEGIN rotateLeft(Node node)
Node tempRightNode = node.getRightNode() // 상위노드의 오른쪽 하위 노드
Node t = tempRightNode.getLeftNode() // 오른쪽 하위 노드의 왼쪽 하위 노드
tempRightNode.setLeftNode(node) // 오른쪽 하위 노드의 왼쪽 하위노드를 상위 노드로 변경
node.setRightNode(t) // 상위 노드의 오른쪽 노드를 왼쪽 하위 노드로 변경
node.updateHeight() // 상위 노드의 높이 변경
tempRightNode.updateHeight() // 오른쪽 하위 노드의 높이 변경
END
2.4.3 Case 3 : 왼쪽 자식노드에 오른쪽 자식 노드만 있을 경우 - LR
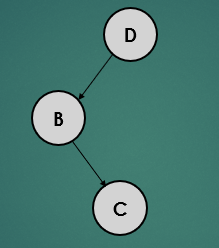
위의 트리를 보면 루트노드는 왼쪽 자신노드만 있고, 왼쪽 자식노드는 오른쪽 자식노드만 있어 불균형 상태이다. 이러한 상태의 트리의 균형을 잡는 과정을 알아보자.
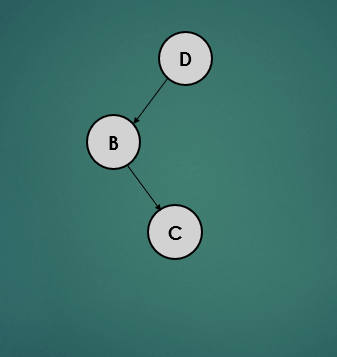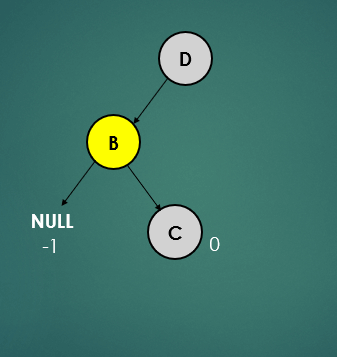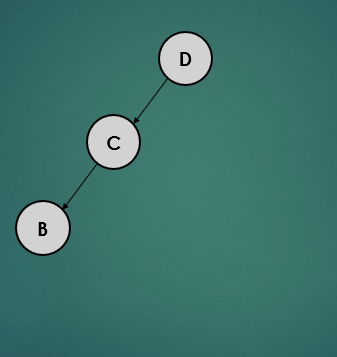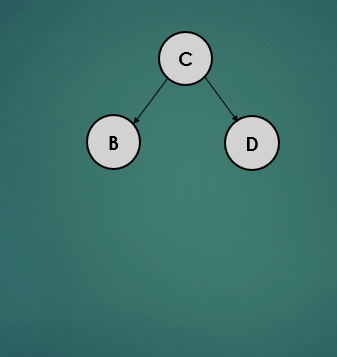
- leaf 노드(C)는 자식 노드가 없기 때문에 왼쪽, 오른쪽 자식노드를 -1로 간주하여 높이를 계산하면 0이 되고, 균형상태이다.
- 노드 B는 왼쪽 자식노드는 null이기때문에 -1, 오른쪽 자식 노드는 0으로 높이를 계산하면 1이 되고, 균형상태이다.
- 루트 노드인 노드 D는 왼쪽 자식노드는 1, 오른쪽 자식노드는 null이기 때문에 -1로 높이를 계산하면 2이기 때문에 불균형 상태이다.
- 노드 B를 왼쪽으로 회전시킨다.
- 이렇게 되면 왼쪽으로 치우친 트리의 형태가 되는데 루트 노드인 D를 오른쪽으로 회전 시킨다.
2.4.4 Case 4 : 오른쪽 자식 노드에 왼쪽 자식 노드만 있을 경우 - RL
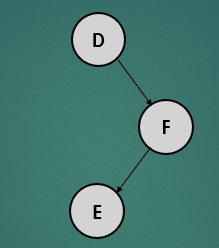
위의 트리를 보면 루트노드는 오른쪽 자신노드만 있고, 오른쪽 자식노드는 왼쪽 자식노드만 있어 불균형 상태이다. 이러한 상태의 트리의 균형을 잡는 과정을 알아보자.
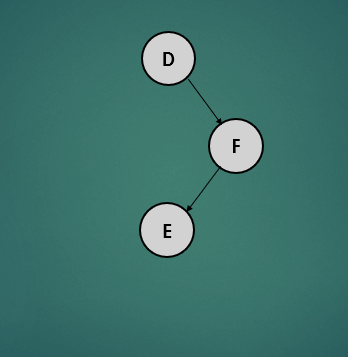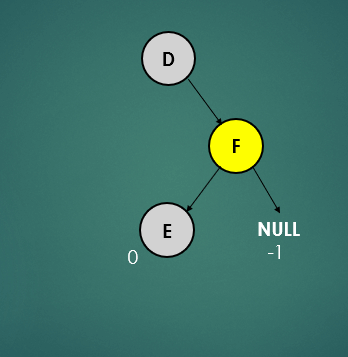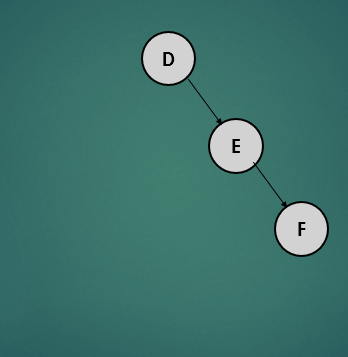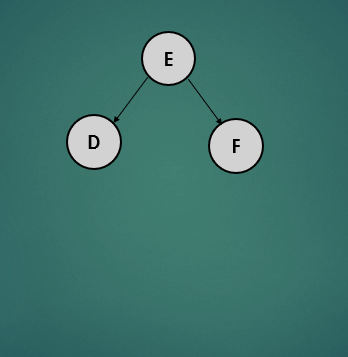
- leaf 노드(E)는 자식 노드가 없기 때문에 왼쪽, 오른쪽 자식노드를 -1로 간주하여 높이를 계산하면 0이 되고, 균형상태이다.
- 노드 F의 왼쪽 자식노드는 1, 오른쪽 자식 노드는 null이기때문에 -1로 높이를 계산하면 1이 되고, 균형상태이다.
- 루트 노드인 노드 D는 왼쪽 자식노드가 null이기때문에 -1, 오른쪽 자식노드 1로 높이를 계산하면 2이기 때문에 불균형 상태이다.
- 노드 F를 오른쪽으로 회전시킨다.
- 이렇게 되면 오른쪽으로 치우친 트리의 형태가 되는데 루트 노드인 D를 왼쪽으로 회전 시킨다.
2.5 삽입(Insert)
AVL 트리의 삽입연산은 2단계로 수행된다. 1단계에서는 이진탐색트리와 동일하게 삽입연산을 수행한다. 2단계에서는 새로 삽입된 노드로부터 루트 노트로 거슬러 올라가며 각 노드의 높이를 갱신한다. 이때 불균형이 발생한 노드를 발견하면 새 노드가 어디에 삽입되었는가에 따라 회전연산을 수행한다.
avlTree.insert(12);
- 이진탐색 트리와 동일하게 삽입연산을 수행한다.
-
삽입연산이 완료되면 삽입한 노드부터 루트노드까지 높이를 계산을 수행하고, 불균형이 발생하면 회전을 수행한다.
-
회전이 끝나고 트리 모든 노드의 높이의 계산을 다시 수행하여, 불균형을 발견하면 회전연산을 다시 수행하고, 더이상 불균형이 없으면 연산을 종료한다.
그렇다면 이번에는 AVL 트리에 처음부터 데이터가 삽입되는 과정을 보자.

avlTree.insert(10);
avlTree.insert(20);
avlTree.insert(30);
avlTree.insert(40);
avlTree.insert(50);
avlTree.insert(60);
2.6 삭제(Remove)
AVL 삭제 연산 또한 마찬가지로 2단계로 수행된다. 1단계에서는 이진탐색트리와 동일하게 삭제연산을 수행한다. 2단계에서는 삭제된 노드로부터 루트 노드 방향으로 거슬러 올라가면서 불균형이 발생한 경우 회전연산을 수행한다.
이진탐색 트리와 동일하게 AVL 트리의 삭제 연산은 아래와 같이 3개의 경우의 수가 존재한다.
- 삭제할 노드가 leaf 노드인 경우
- 삭제할 노드가 한 개의 자식 노드를 가진 경우
- 삭제할 노드가 두 개의 자식 노드를 가진 경우
2.6.1 : 삭제할 노드가 leaf 노드일 경우
제거할 노드가 leaf 노드일 경우는 아래와 간단하게 제거하기만 하면 된다.
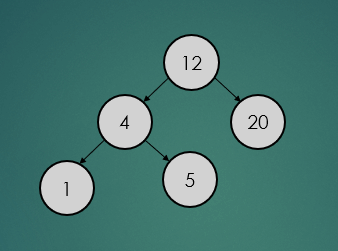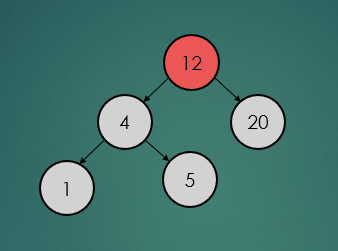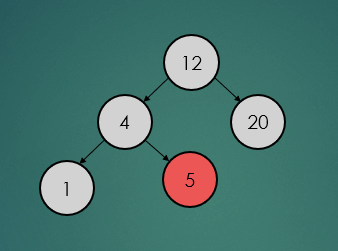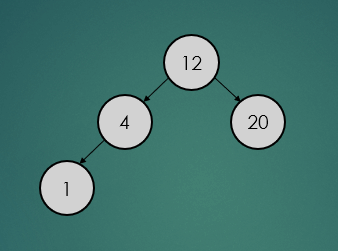
avlTree.remove(5);
2.6.2 : 삭제할 노드가 한 개의 자식노드를 가진 경우
제거할 노드가 하나의 자식 노드를 가진 경우는 아래와 같이 참조값을 변경하기만 하면 된다.
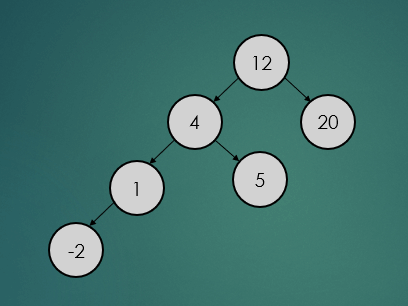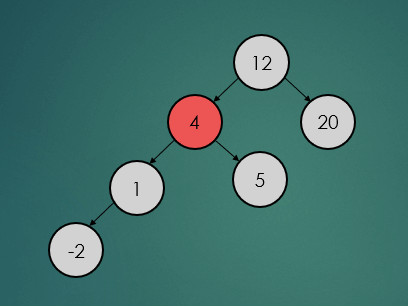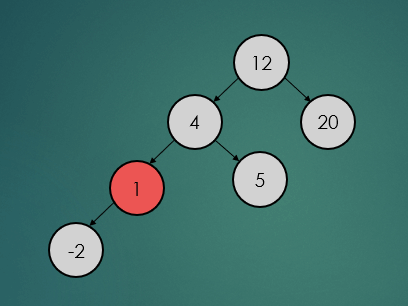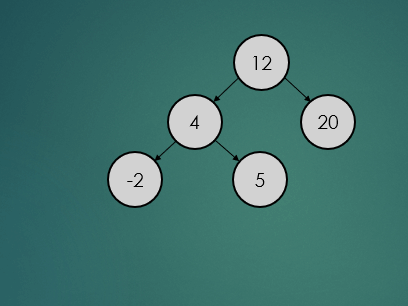
avlTree.remove(1);
2.6.3 : 삭제할 노드가 두 개의 자식노드를 가진 경우
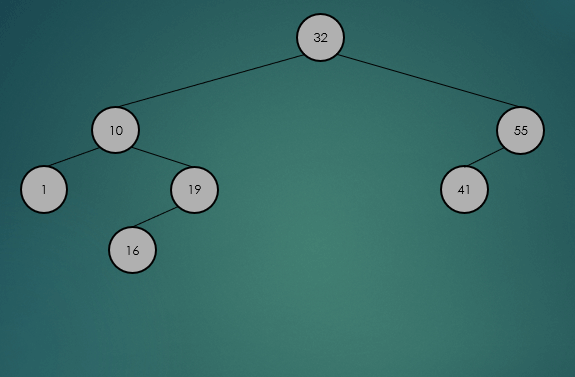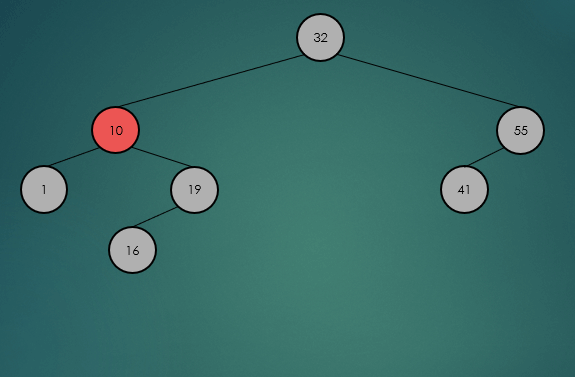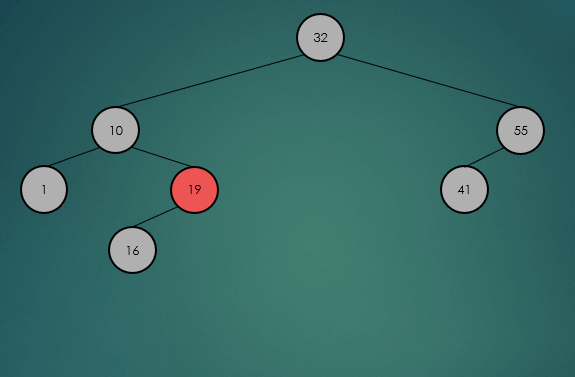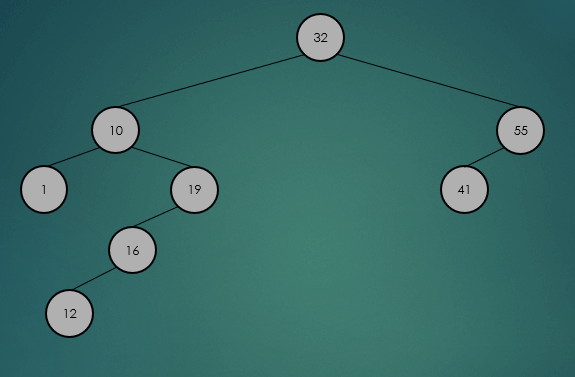
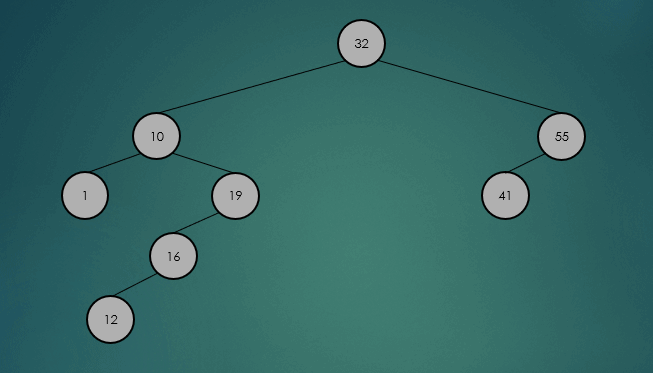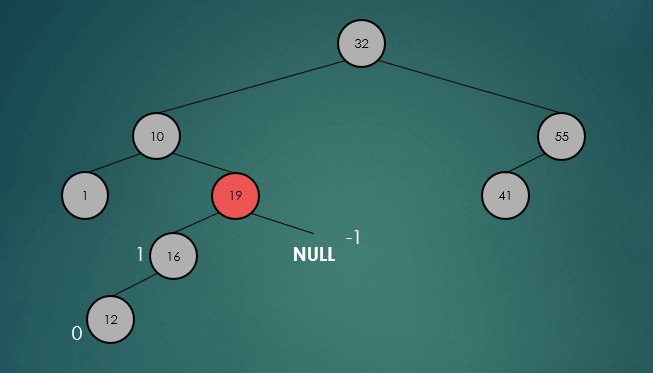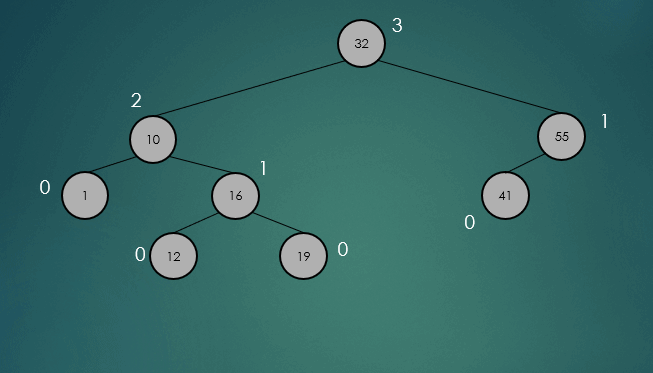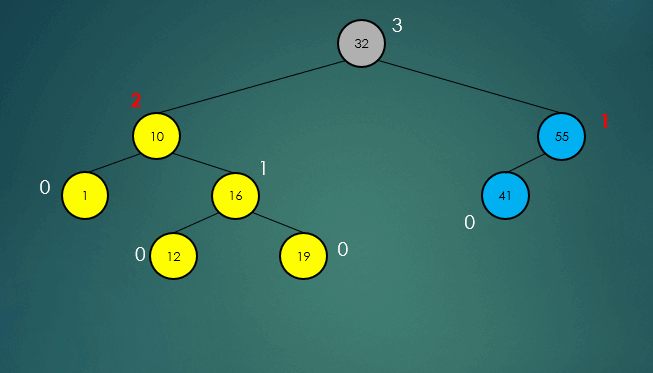
제거할 노드가 2개의 자식 노드를 가진 경우 왼쪽 하위 트리에서 가장 큰 항목 또는 오른쪽 하위 트리에서 가장 작은 항목을 찾아 서로의 위치를 바꾸고, 노드를 제거한다.
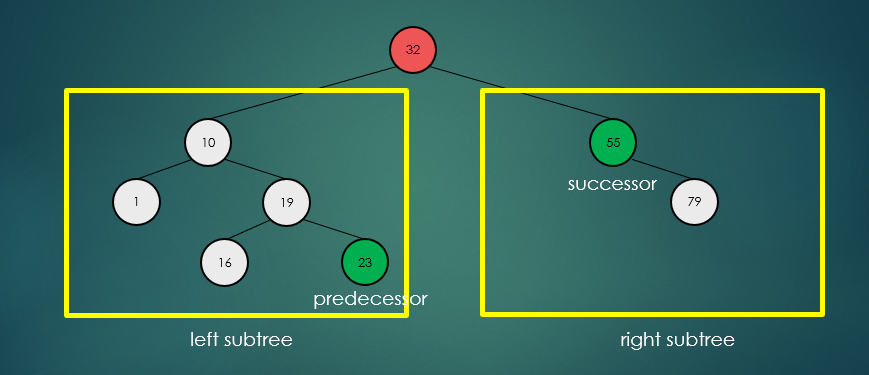
왼쪽 하위 트리에서 가장 큰 항목을 찾아 제거했을 경우
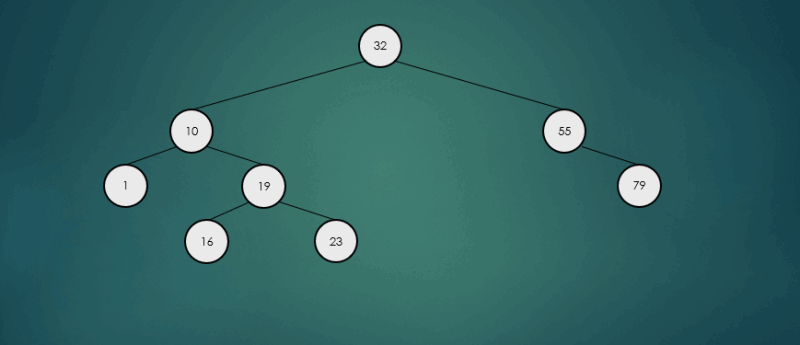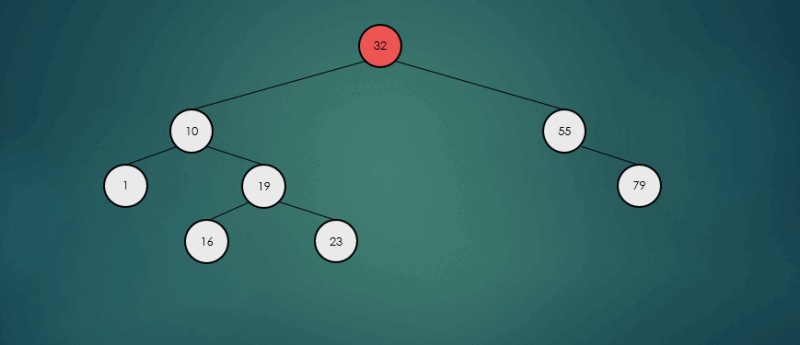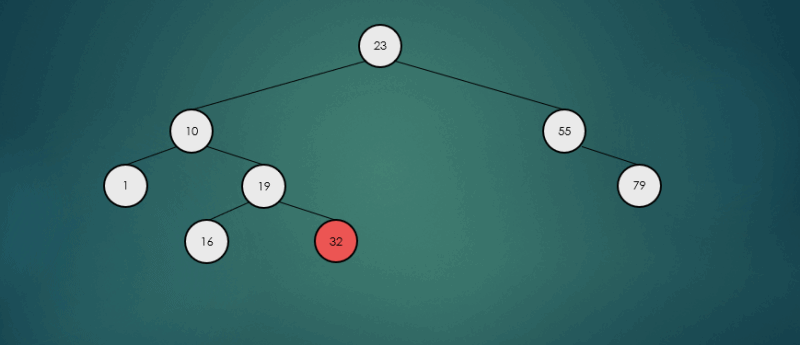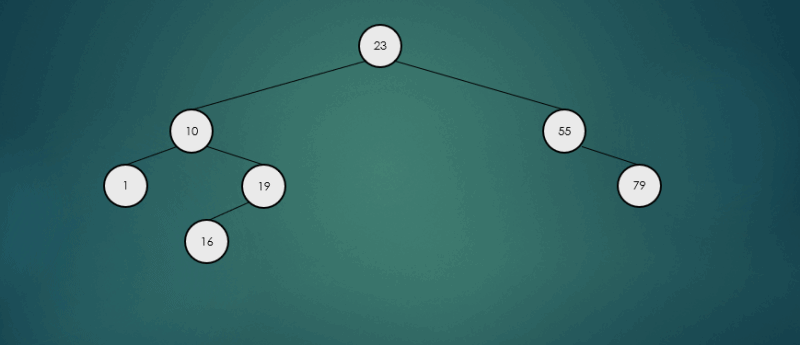
오른쪽 하위 트리에서 가장 큰 항목을 찾아 제거했을 경우
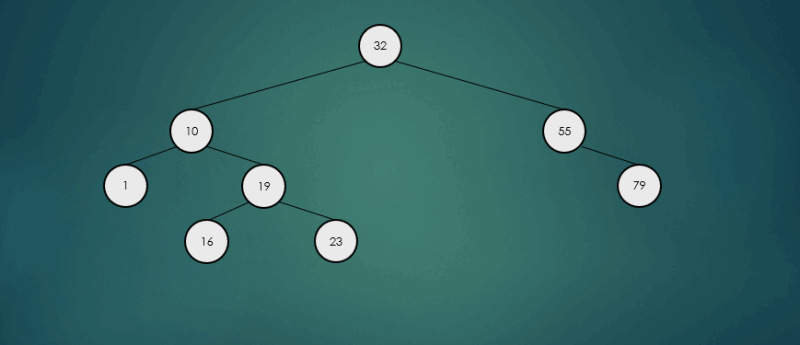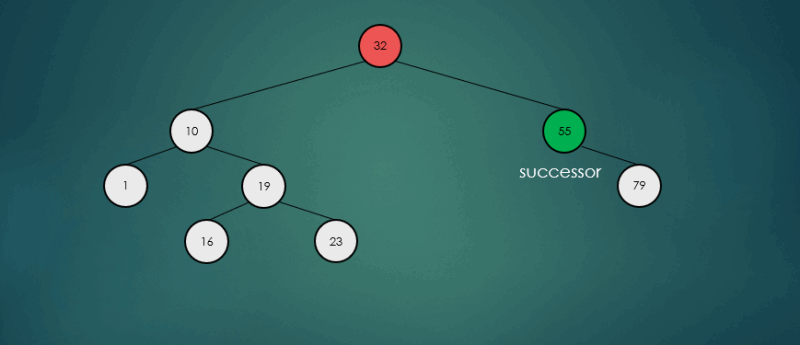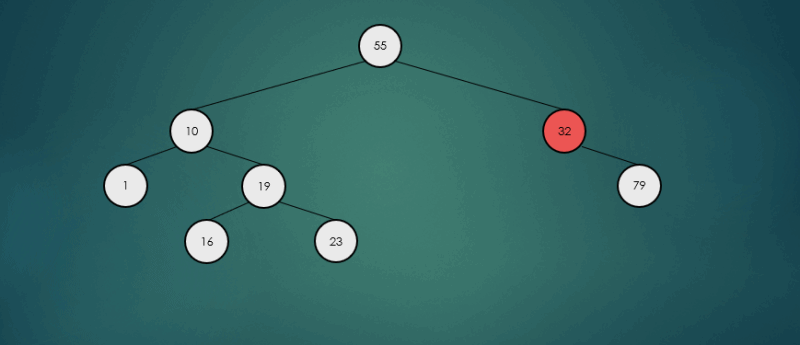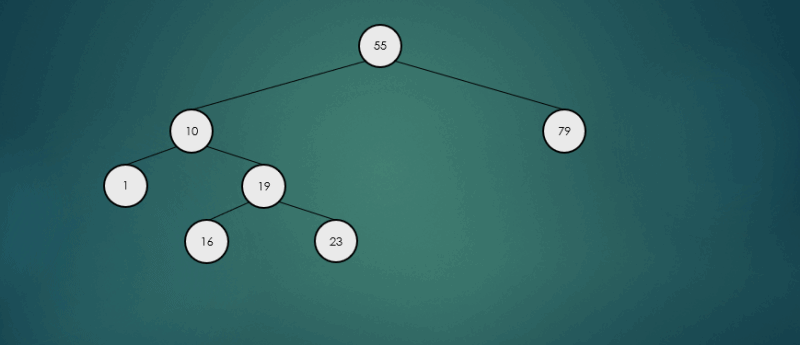
avlTree.remove(32);
2.6.4 : 노드를 삭제 한 뒤 트리가 불균형일 때
노드를 삽입할 때와 마찬가지로 노드를 삭제한 뒤 트리가 불균형인지 확인한 뒤 불균형 상태라면 회전연산을 수행한다.
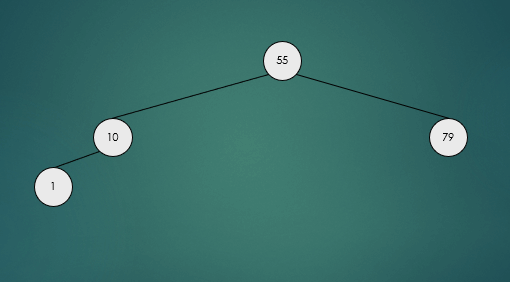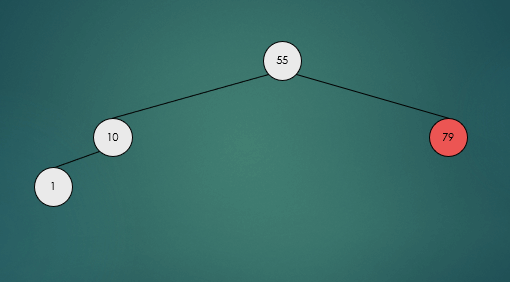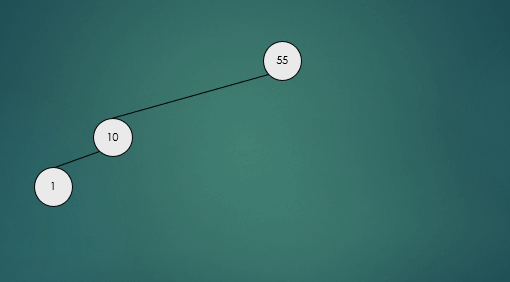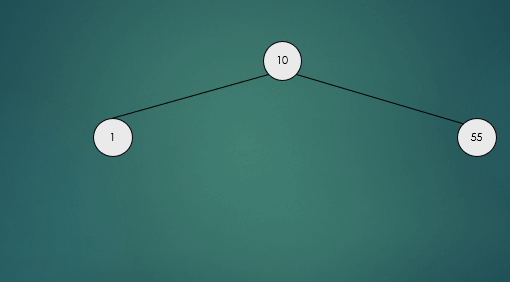
avlTree.remove(79);
3. AVL Tree 구현
3.1 클래스 작성
기본적으로 AVL Tree를 구현하기 위해 노드 클래스, 트리 인터페이스, 트리 인터페이스를 구현한 AVL 트리 클래스를 작성해준다.
// 노드 클래스
public class Node<T> {
private T data; // 데이터
private Node<T> leftNode; // 왼쪽 하위노드
private Node<T> rightNode; // 오른쪽 하위노드
private int height; // 높이
public Node(T data) {
this.data = data;
}
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
public Node<T> getLeftNode() {
return leftNode;
}
public void setLeftNode(Node<T> leftNode) {
this.leftNode = leftNode;
}
public Node<T> getRightNode() {
return rightNode;
}
public void setRightNode(Node<T> rightNode) {
this.rightNode = rightNode;
}
public int getHeight() {
return height;
}
public void setHeight(int height) {
this.height = height;
}
@Override
public String toString() {
return this.data.toString();
}
}
// 트리 인터페이스
public interface Tree<T> {
public void insert(T data); // 삽입
public void traverse(); // 순회
public void delete(T data); // 삭제
}
// AVL 트리 클래스
public class AVLTree2<T extends Comparable<T>> implements Tree<T> {
private Node<T> root; // 루트 노드
// 삽입
@Override
public void insert(T data) {
}
// 순회
@Override
public void traverse() {
}
// 삭제
@Override
public void delete(T data) {
}
}
3.2 회전
// 특정 노드의 높이 반환
private int height(Node<T> node) {
if (node == null) {
return -1;
}
return node.getHeight();
}
회전을 수행하기 위해서는 노드의 높이들을 알기 위해 위와 같이 AVL 트리 클래스에 특정노드의 높이를 반환하는 메서드를 작성한다.
// 오른쪽 회전
private Node<T> rightRotation(Node<T> parentNode) {
System.out.println("Rotating to the right on node : " + parentNode);
Node<T> newParentNode = parentNode.getLeftNode(); // 왼쪽 자식노드가 새로운 부모노드가 됨
Node<T> nullNode = newParentNode.getRightNode(); // 왼쪽 자식노드의 오른쪽 자식노드(null 노드)
newParentNode.setRightNode(parentNode); // 새로운 부모노드의 오른쪽 자식노드에 기존의 부모노드를 세팅
parentNode.setLeftNode(nullNode); // 기존의 부모노드의 왼쪽 자식노드를 null 노드로 세팅
// 회전한 노드들의 높이 갱신
parentNode.setHeight(Math.max(height(parentNode.getLeftNode()), height(parentNode.getRightNode())) + 1);
newParentNode.setHeight(Math.max(height(newParentNode.getLeftNode()), height(newParentNode.getRightNode())) + 1);
// 새로운 부모노드 반환
return newParentNode;
}
// 왼쪽 회전
private Node<T> leftRotation(Node<T> parentNode) {
System.out.println("Rotating to the left on node : " + parentNode);
Node<T> newParentNode = parentNode.getRightNode(); // 오른쪽 자식노드가 새로운 부모노드가 됨
Node<T> nullNode = newParentNode.getLeftNode(); // 오른쪽 자식노드의 왼쪽 자식노드(null 노드)
newParentNode.setLeftNode(parentNode); // 새로운 부모노드의 왼쪽 자식노드에 기존의 부모노드를 세팅
parentNode.setRightNode(nullNode); // 기존의 부모노드의 오른쪽 자식노드를 null 노드로 세팅
// 회전한 노드들의 높이 갱신
parentNode.setHeight(Math.max(height(parentNode.getLeftNode()), height(parentNode.getRightNode())) + 1);
newParentNode.setHeight(Math.max(height(newParentNode.getLeftNode()), height(newParentNode.getRightNode())) + 1);
// 새로운 부모노드 반환
return newParentNode;
}
3.3 삽입
삽입 메서드를 아래와 같이 작성해준다. 삽입 과정은 이진탐색 트리와 동일하게 처리하지만 삽입 연산이 완료되고, 트리의 노드들의 높이를 계산하여 트리가 불균형인지 판단하여 불균형이라면 회전연산을 수행한다.
// 삽입
@Override
public void insert(T data) {
root = insert(root, data);
}
// 삽입 구현
private Node<T> insert(Node<T> node, T data) {
// root가 비어있거나 leaf 노드인 경우 새로운 노드 생성
if (node == null) {
return new Node<>(data);
}
// 삽입할 데이터가 상위노드(부모노드)의 데이터보다 작으면 왼쪽 하위노드에 새로운 노드 생성
// 삽입할 데이터가 상위노드(부모노드)의 데이터보다 크면 오른쪽 하위노드에 새로운 노드 생성
if (data.compareTo(node.getData()) < 0) {
node.setLeftNode(insert(node.getLeftNode(), data)); // 왼쪽 leaf 노드를 찾을때까지 재귀호출
} else {
node.setRightNode(insert(node.getRightNode(), data)); // 오른쪽 leaf 노드를 찾을 때까지 재귀 호출
}
// 삽입이 완료되고 노드의 높이를 갱신
node.setHeight(Math.max(height(node.getLeftNode()), height(node.getRightNode())) + 1);
// 삽입으로 인해 트리가 불균형이면 회전연산(LL, RR, LR, RL) 수행
node = settleViolation(data, node);
return node;
}
// 회전 수행 : 삽입시
private Node<T> settleViolation(T data, Node<T> node) {
// 트리의 불균형 여부 파악
int balance = getBalance(node);
// Left-Left : 높이 차이가 1보다 크고, 삽입된 데이터가 상위노드의 데이터보다 작은 경우
if (balance > 1 && data.compareTo(node.getData()) < 0) {
System.out.println("Tree is left-left heavy.");
return rightRotation(node); // 오른쪽 회전 수행
}
// Right-Right : 높이 차이가 -1보다 작고, 삽입된 데이터가 상위노드의 데이터보다 큰 경우
if (balance < -1 && data.compareTo(node.getData()) > 0) {
System.out.println("Tree is right-right heavy.");
return leftRotation(node); // 왼쪽 회전 수행
}
// Left-Right : 높이 차이가 1보다 크고, 삽입된 데이터가 상위노드의 데이터보다 큰 경우
if (balance > 1 && data.compareTo(node.getData()) > 0) {
System.out.println("Tree is left-right heavy.");
node.setLeftNode(leftRotation(node.getLeftNode())); // 왼쪽 회전 수행
return rightRotation(node); // 오른쪽 회전 수행
}
// Right-Left : 높이 차이가 -1보다 작고, 삽입된 데이터가 상위노드의 데이터보다 작은 경우
if (balance < -1 && data.compareTo(node.getData()) < 0) {
System.out.println("Tree is right-left heavy.");
node.setRightNode(rightRotation(node.getRightNode())); // 오른쪽 회전 수행
return leftRotation(node); // 왼쪽 회전 수행
}
return node;
}
// 트리 균형/불균형 여부 판단
private int getBalance(Node<T> node) {
// 트리가 비어있는 상태
if (node == null) {
return 0;
}
// 계산 결과가 1보다 큰 경우 : LL or LR
// 계산 결과가 -1보다 작은 경우 : RR or RL
return height(node.getLeftNode()) - height(node.getRightNode());
}
3.4 순회
AVL 트리는 이진탐색 트리의 순회와 같다.
// 순회
@Override
public void traverse() {
if (root == null) {
return;
}
System.out.print("inorder traversal : ");
inOrderTraversal(root);
System.out.println();
System.out.print("preorder traversal : ");
preOrderTraversal(root);
System.out.println();
System.out.print("postorder traversal : ");
postOrderTraversal(root);
}
// 중위 순회
private void inOrderTraversal(Node<T> node) {
if (node.getLeftNode() != null) {
inOrderTraversal(node.getLeftNode());
}
System.out.print(node + " ==> ");
if (node.getRightNode() != null) {
inOrderTraversal(node.getRightNode());
}
}
// 전위 순회
private void preOrderTraversal(Node<T> node) {
System.out.print(node + " ==> ");
if (node.getLeftNode() != null) {
inOrderTraversal(node.getLeftNode());
}
System.out.print(node + " ==> ");
if (node.getRightNode() != null) {
inOrderTraversal(node.getRightNode());
}
}
// 후위 순회
private void postOrderTraversal(Node<T> node) {
if (node.getLeftNode() != null) {
inOrderTraversal(node.getLeftNode());
}
if (node.getRightNode() != null) {
inOrderTraversal(node.getRightNode());
}
System.out.println(node);
}
3.5 삭제
삭제 연산은 아래와 같이 코드를 작성하면된다. 삭제 연산도 이진탐색트리와 동일하지만 삭제 연산이 완료되면 트리의 각노드의 높이를 계산해 트리의 불균형이 발생한 경우 각각의 상황에 맞게 회전연산을 수행한다.
// 삭제
@Override
public void delete(T data) {
root = delete(root, data);
}
// 삭제 구현
private Node<T> delete(Node<T> node, T data) {
if (node == null) {
return node;
}
// 삭제할 노드 탐색
// 삭제할 노드의 데이터가 부모노드의 데이터보다 작은 경우
if (data.compareTo(node.getData()) < 0) {
node.setLeftNode(delete(node.getLeftNode(), data)); // 왼쪽 자식노드 방향으로 삭제 재귀호출
// 삭제할 노드의 데이터가 부모노드의 데이터보다 큰 경우
} else if (data.compareTo(node.getData()) > 0) {
node.setRightNode(delete(node.getRightNode(), data)); // 오른쪽 자식노드 방향으로 삭제 재귀호출
// 삭제할 노드를 찾은 경우
} else {
// 1. 삭제할 노드가 leaf 노드인 경우
if (node.getLeftNode() == null && node.getRightNode() == null) {
System.out.println("Removing a leaf node...");
return null;
}
// 2. 삭제할 노드가 하나의 자식노드를 가진 경우
if (node.getLeftNode() == null) {
System.out.println("Removing the right child node");
Node<T> tempNode = node.getRightNode();
node = null;
return tempNode;
} else if (node.getRightNode() == null) {
System.out.println("Removing the left child node");
Node<T> tempNode = node.getLeftNode();
node = null;
return tempNode;
}
// 3. 삭제할 노드가 두개의 자식노드를 가진 경우
System.out.println("Removing item with the children");
Node<T> tempNode = getPredecessor(node.getLeftNode()); // 왼쪽 자식노드 중에서 가장 큰 노드
node.setData(tempNode.getData()); // 삭제할 노드의 데이터와 가장 큰 노드의 데이터 교환
node.setLeftNode(delete(node.getLeftNode(), tempNode.getData())); // 삭제 재귀호출
}
// 높이 갱신
node.setHeight(Math.max(height(node.getLeftNode()), height(node.getRightNode())) + 1);
// 삭제 완료후 트리 불균형 체크, 회전 수행
return settleDeletion(node);
}
// 회전 수행 : 삭제시
private Node<T> settleDeletion(Node<T> node) {
int balance = getBalance(node);
// Left-Left or Left-Right 인 경우
if (balance > 1) {
// Left-Right
if (getBalance(node.getLeftNode()) < 0) {
node.setLeftNode(leftRotation(node.getLeftNode())); // 왼쪽 회전
}
return rightRotation(node); // 오른쪽 회전
}
// Right-Right or Right-Left 인 경우
if (balance < -1) {
// Right-Left
if (getBalance(node.getRightNode()) > 0) {
node.setRightNode(rightRotation(node.getRightNode())); // 오른쪽 회전
}
return leftRotation(node); // 왼쪽 회전
}
return node;
}
3.6 테스트
// 테스트 클래스
public class App {
public static void main(String[] args) {
Tree<String> avlTree = new AVLTree<>();
avlTree.insert("A");
avlTree.insert("B");
avlTree.insert("C");
avlTree.insert("D");
avlTree.insert("E");
avlTree.traverse();
avlTree.delete("D");
avlTree.traverse();
}
}
// 실행결과
Tree is right-right heavy.
Rotating to the left on node : A
Tree is right-right heavy.
Rotating to the left on node : C
inorder traversal : A ==> B ==> C ==> D ==> E ==>
preorder traversal : B ==> A ==> B ==> C ==> D ==> E ==>
postorder traversal : A ==> C ==> D ==> E ==> B
Removing item with the children
Removing a leaf node...
inorder traversal : A ==> B ==> C ==> E ==>
preorder traversal : B ==> A ==> B ==> C ==> E ==>
postorder traversal : A ==> C ==> E ==> B