더블에스 Devlog

자료구조 - Binary Heap

 
  • 2018년 11월 07일

본 글은 Udemy의 자바 자료구조 강의를 듣고 개인적으로 학습한 내용 복습하기 위해 작성된 글로 내용상 오류가 있을 수 있습니다. 오류가 있다면 지적 부탁 드리겠습니다.

1. Priority Queue(우선순위큐)란?

이진힙을 알아보기에 앞서 우선순위큐에 대해 알아보자.

우선순위큐눈 가장 높은 우선순위를 가진 항목에 접근하거나 해당 항목을 삭제하는 연산과 임의의 우선순위를 가진 항목을 삽입하는 연산을 지원하는 자료구조이다. 스택, 큐는 일종의 우선순위큐이다.

우선순위큐의 특징은 아래와 같다.

  • 모든 항목에는 추가 속성이 있는데 이것을 우선순위 값(priority value)라고 한다.
  • 우선순위 큐에서는 우선순위가 높은 요소는 우선순위가 낮은 요소보다 먼저 처리된다.
  • 우선순위 큐는 일반적으로 일반적으로 힙으로 구현되기도 하지만 자체 균형트리(self balancing tree)로도 구현될 수 있다.

2. Heap이란?

2.1 Heap의 기본 개념

Heap은 완전 이진 트리로서 부모의 우선순위가 자식의 우선순위보다 높은 자료구조이다. 이진트리와 달리 상위 노드보다 작은 값을 왼쪽 하위 노드에 큰 값을 오른쪽 하위 노드에 놓지 않는다. 즉, 삽입되는 데이터 순서대로 왼쪽, 오른쪽 하위노드에 위치시킨다.

binary-heap-complete-binary-tree

이진힙은 Max Heap, Min Heap 2가지 종류가 있다.

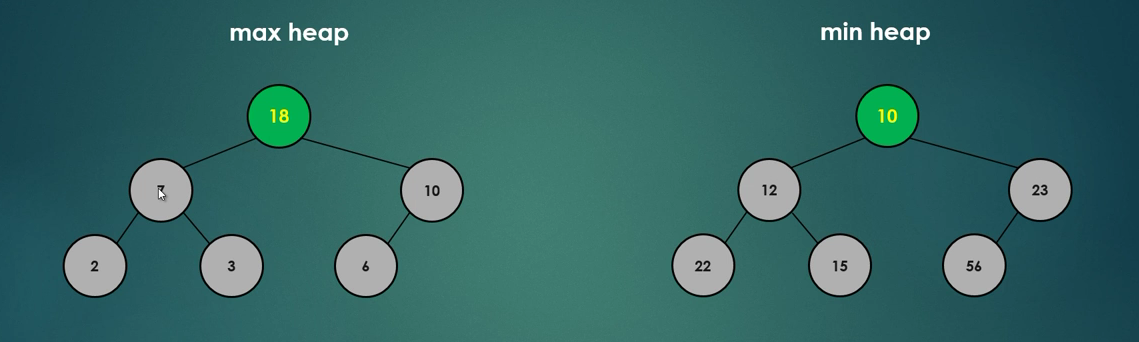
max-heap-min-heap

  • Max Heap : 상위 노드의 키 >= 하위 노드의 키, 최상위 키가 루트 노드
  • Min Heap : 상위 노드의 키 <= 하위 노드의 키, 최하위 키가 루트 노드

2.2 Array로 Heap표현

완전 이진 트리는 1차원 배열로 구현할 수 있는데 아래의 그림은 최대 힙을 나타낸 것으로 배열의 인덱스를 루트 노드부터 하위노드까지 차례로 채워나간 것을 확인할 수 있다.

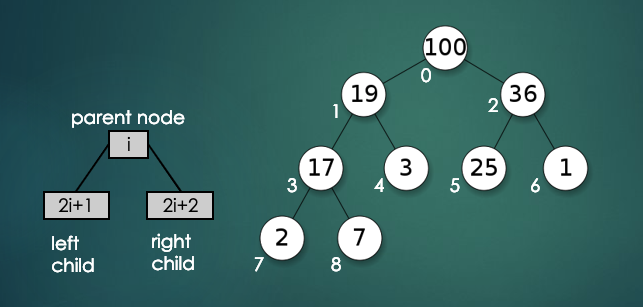
max-heap-array-presentation

그리고 위의 그림에서 볼 수 있듯이 상위노드의 인덱스를 통해 하위노드들의 인덱스를 계산하는 방법은 아래와 같다.

왼쪽 하위노드의 인덱스 = 부모노드의 인덱스 * 2 + 1
오른쪽 하위노드의 인덱스 = 부모노드의 인덱스 * 2 + 2

2.3 Heap의 연산

2.3.1 삽입

heap에 데이터를 삽입하고 heap속성을 충족하는지 확인한 뒤 위반할 경우 heap 속성을 충족하도록 재구성을 하게 된다.

max-heap-insert

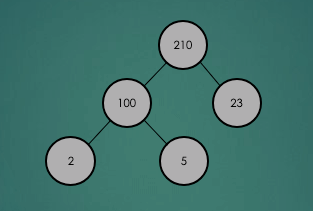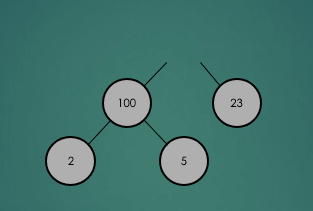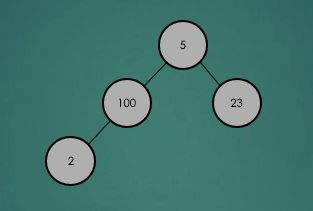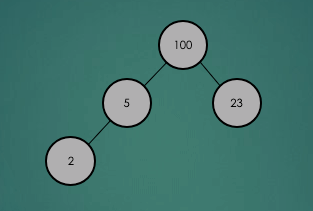
2.3.2 삭제

삭제하려는 항목을 제거한 뒤 그 자리에 마지막 항목을 놓고 다시 heap 속성이 충족되는지 확인하고 재구성을 한다.

max-heap-remove

2.4 Heap 정렬

힙정렬은 힙 자료구조를 이용하는 알고리즘이다. 먼저 배열에 저장된 데이터의 키를 우선순위로 최대힙을 만들고, 이후 루트 노드와 가장 마지막 노드에 있는 데이터를 교환한 후 힙의 크기를 1 감소시킨다. 루트노드로 이동한 숫자로 인해 위배된 heap속성을 충족하도록 재구성한다. 이러한 과정을 반복하여 나머지 항목들을 정렬해나간다.

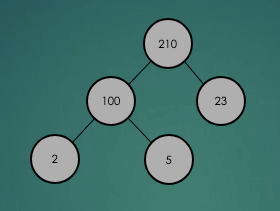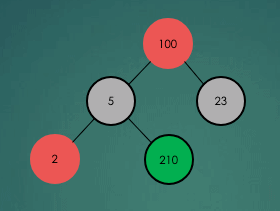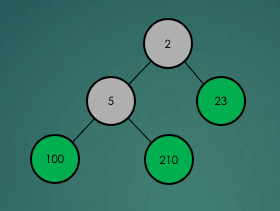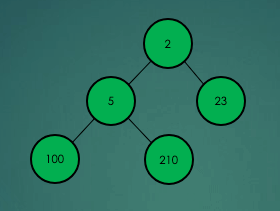
heapsort

3. Heap 구현 코드

3.1 Heap 클래스 작성

public class Heap {

    private int[] heap;     // heap
    private int heapSize;   // heap 사이즈

    // 생성자
    public Heap(int capacity) {
        this.heap = new int[capacity];
    }

    // heap 출력
    public void printHeap() {
        System.out.print("[ ");
        for (int i = 0; i < heapSize; i++) {
            System.out.print( heap[i] + " ");
        }
        System.out.print("]");
        System.out.println();
    }
}

3.2 삽입 관련 메서드 작성

// 삽입
// running time : 삽입은 O(1)이 걸리지만 heap 속성을 위반한 경우 fixUp()를 수행해야 하기 때문에 O(logN)
public void insert(int item) {

    // heap이 차있는지 체크
    if (isHeapFull()) {
        throw new RuntimeException("Heap is full...");
    }

    this.heap[heapSize] = item; // 항목 삽입
    heapSize = heapSize + 1;    // 사이즈 증가
    fixUp(heapSize - 1); // heap 속성을 위반한 경우 heap 속성 재구성

}

// heap이 차있는지 체크
private boolean isHeapFull() {
    return this.heap.length == this.heapSize;
}

// heap 속성을 위반한 경우 heap 속성을 유지하기 위해 교환 수행
// running time : O(logN)
private void fixUp(int currentIndex) {

    int parentIndex = (currentIndex - 1) / 2; // 상위 노드의 인덱스 계산

    // 루트노드가 아니고, 상위노드보다 햔제노드가 클 경우
    if (currentIndex > 0 && heap[currentIndex] > heap[parentIndex]) {
        swap(currentIndex, parentIndex); // 현재 노드와 상위 노드 교환 수행
        fixUp(parentIndex); // 루트노드까지 반복 수행하기 위해 재귀 호출
    }

}

// 노드의 교환 수행
private void swap(int index1, int index2) {
    int temp = heap[index1];
    heap[index1] = heap[index2];
    heap[index2] = temp;
}

Heap의 삽입은 아래와 같은 과정을 거치게 된다.

  1. 배열 heap이 차있다면 RuntimeException을 던지고, 그렇지 않다면 삽입을 수행한다.
  2. 항목을 삽입하고, 배열의 사이즈 변수인 heapSize을 1증가 시킨다.
  3. fixUp()메서드를 통해 새로 삽입된 항목으로 인해 heap 속성을 위반하는지 확인하고, 위반한 경우 heap 속성을 재구성 작업을 수행한다.

3.2 삭제 관련 메서드

// heap 최대값 반환
// running time : O(1)
public int getMax() {
    return this.heap[0];
}

// heap 최대값 반환 + 항목 제거
// running time : 0(logN)
public int poll() {
    int max = getMax();     // 최대값
    swap(0, heapSize - 1);  // 최상위 노드와 최하위노드 교환
    this.heapSize--;        // heap 사이즈 감소
    fixDown(0);       // heap 속성을 위반할 경우 heap 속성 재구성
    return max;
}

// heap 속성을 위반한 경우 교환 수행
private void fixDown(int index) {

    int indexLeft = 2 * index + 1;  // 왼쪽 하위노드 인덱스 계산
    int indexRight = 2 * index + 2; // 오른쪽 하위노드 인덱스 계산
    int indexLargest = index;       // 상위 노드의 인덱스

    // 왼쪽 하위노드가 상위노드보다 큰 경우
    if (indexLeft < heapSize && heap[indexLeft] > heap[index]) {
        indexLargest = indexLeft;
    }

    // 오른쪽 하위노드가 왼쪽 하위노드보다 큰 경우
    if (indexRight < heapSize && heap[indexRight] > heap[indexLargest]) {
        indexLargest = indexRight;
    }

    // 왼쪽 or 오른쪽 하위노드가 상위노드보다 큰 경우
    if (index != indexLargest) {
        swap(index, indexLargest); // 교환 수행
        fixDown(indexLargest);     // 최하위 노드까지 반복수행하기 위해 재귀 호출
    }

}

Heap의 삭제 과정은 아래와 같다.

  1. getMax()메서드를 통해 얻은 최대값을 변수 max에 저장한다.
  2. 최상위(루트) 노드와 최하위 노드를 교환한다.
  3. heap 사이즈를 감소시킨다.
  4. heap 속성을 위반할 경우 heap 속성을 재구성하기 위해 루트노트부터 최하위 노드까지 재구성을 수행한다.

3.3 정렬

// 힙정렬
public void heapsort() {
    int size = this.heapSize;
    System.out.print("[ ");
    // 힙 사이즈 만큼 반복수행
    for (int i = 0; i < size; i++) {
        int max = poll();            // 현재 heap의 최대값 추출
        System.out.print(max + " "); // 최대값 출력
    }
    System.out.print("]");
}

3.4 테스트 결과

public class App {
    public static void main(String[] args) {

        Heap heap = new Heap(8); // 힙 생성

        // 삽입
        heap.insert(20);
        heap.insert(4);
        heap.insert(45);
        heap.insert(11);
        heap.insert(7);
        heap.insert(33);
        heap.insert(70);
        heap.insert(35);

        // 힙 출력
        heap.printHeap();

        // 힙 최대값 반환
        System.out.println(heap.getMax());

        // 힙 삭제
        System.out.println(heap.poll());

        // 힙 출력
        heap.printHeap();

        // 힙 정렬
        heap.heapsort();
    }
}

[ 70 35 45 11 7 20 33 4 ]
70
70
[ 45 35 33 11 7 20 4 ]
[ 45 35 33 20 11 7 4 ]
검색