더블에스 Devlog

자료구조 - Ternary Search Tree

 
  • 2019년 03월 08일

1. Trie와 TST(Ternary Search Tree) 비교 및 특징

tst-pic

  • Trie는 탐색, 정렬에 매우 효율적이지만 메모리를 많이 사용하는 문제가 있다.
  • TST는 Trie에 비해 적은 reference와 null object를 가진다.
  • Trie와 마찬가지로 TST도 노드에 문자열을 저장한다.
  • TST는 각 노드마다 3개의 하위노드를 가진다.
    • less : lower child
    • equal : middle child
    • greater : higher child
  • 해시맵 만큼 효율적이다.
  • 해싱은 전체 문자열의 키를 탐색해야하지만 TST는 그렇지 않다.
  • TST도 정렬 연산을 수행할 수 있다.
  • TST는 해시맵보다 빠르며 BST보다 유연하다.

2. TST 연산

2.1 삽입

TST의 삽입 연산은 아래와 같이 이루어진다.

2.1.1 “cat”문자열의 키를 가진 데이터 삽입

tst-insert-cat

put("cat", 23);

TST에 데이터가 존재하지 않을 경우 Trie와 같은 방식으로 차례로 문자열에서 문자 하나씩 가운데 노드에 차례로 삽입이 된다. 하지만 루트노드에 빈 문자열을 저장하지 않고 바로 첫번째 문자를 루트노드부터 삽입하는 것이 Trie와 차이점이다.

2.1.2 “apple”문자열의 키를 가진 데이터 삽입

tst-insert-apple

put("apple", 46);

apple의 문자열 첫번째 a가 c보다 작기 때문에 c의 왼쪽 하위트리로 삽입되고, 나머지 문자열들은 하나씩 차례로 가운데 노드에 삽입된다.

2.1.3 “car”문자열의 키를 가진 데이터 삽입

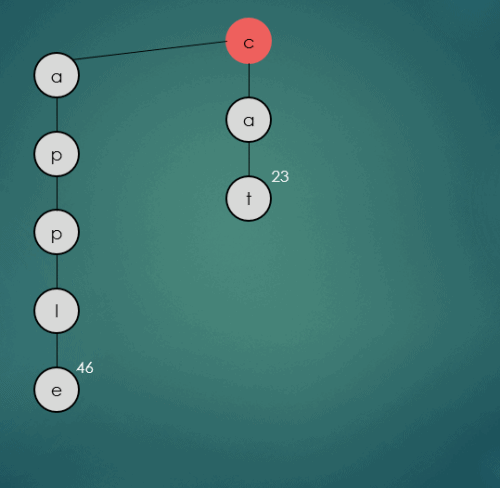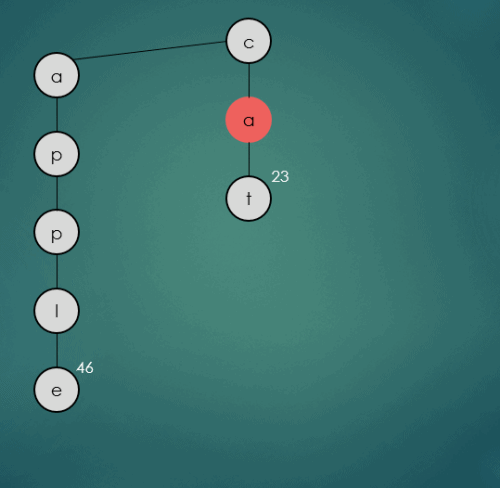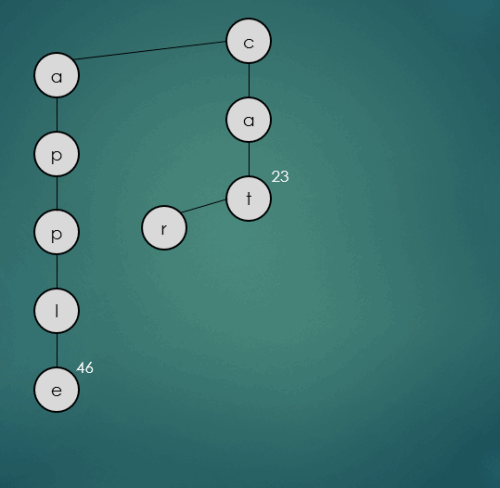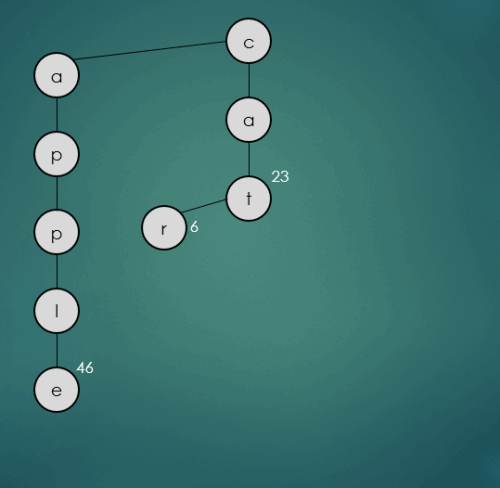
tst-insert-car

put("car", 6);

car는 기존에 삽입된 cat과 첫번째, 두번째 문자열이 동일하기 때문에 그대로 가운데 하위 트리를 따라 이동한다. 세번째 문자열 r은 기존에 삽입된 t보다 작기 때문에 오른쪽 하위노드로 삽입된다.

2.1.4 “carrot”문자열의 키를 가진 데이터 삽입

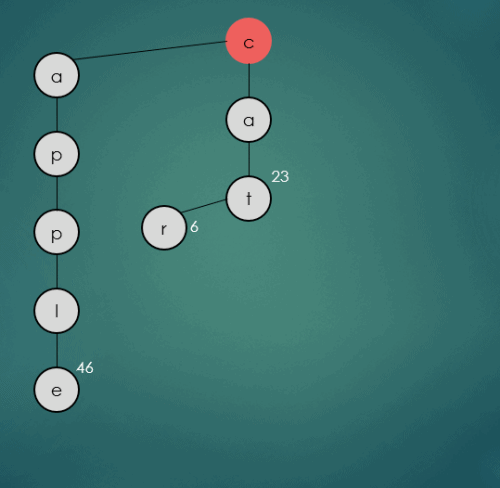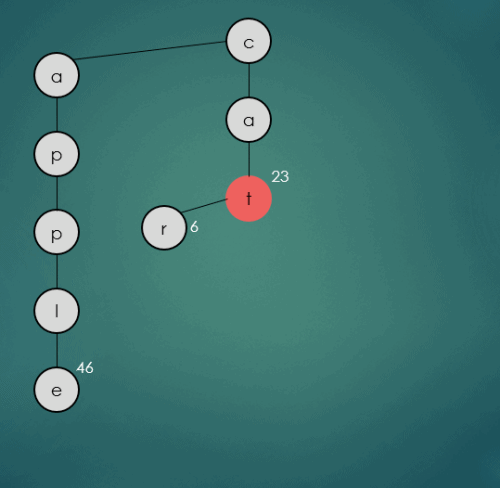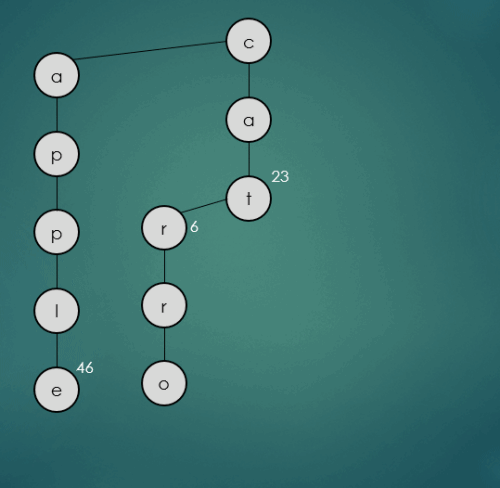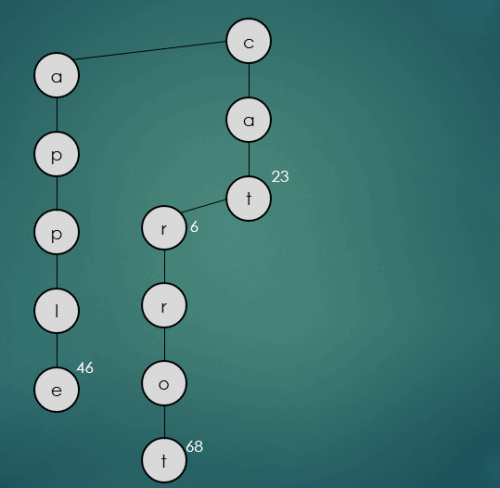
tst-insert-carrot

put("carrot", 68);

carrot은 기존에 삽입된 cat과 첫번째, 두번째 문자열이 동일하기 때문에 그대로 가운데 하위 트리를 따라 이동한다. 세번째 문자열은 기존에 삽입된 car의 세번째 문자열과 동일하기 때문에 그대로 가운데 노드로 이동하고 나머지 문자열은 rot는 차례로 하나씩 가운데 하위노드에 삽입된다.

2.1.5 “cow”문자열의 키를 가진 데이터 삽입

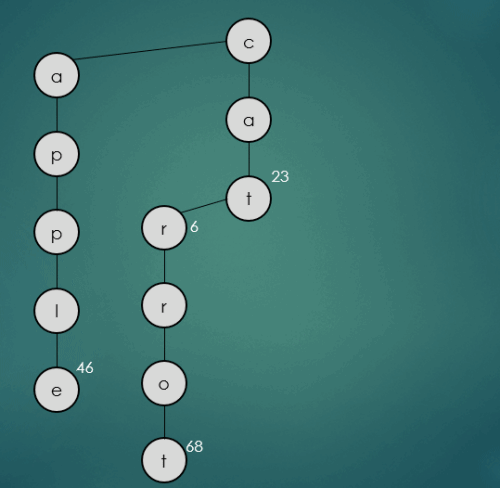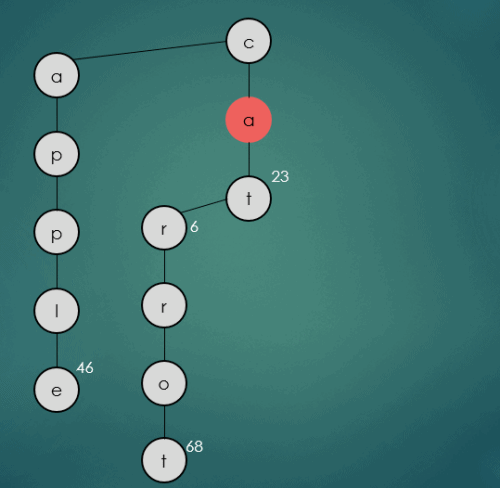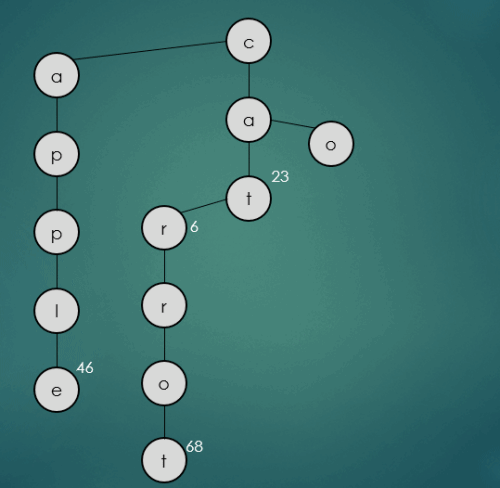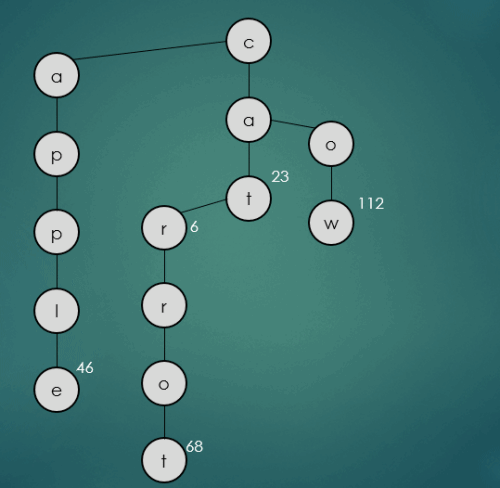
tst-insert-cow

put("cow", 112);

cow는 기존에 삽입된 cat과 첫번째 문자열만 동일하기 때문에 cat의 두번째 문자열 a와 cow의 두번째 문자열 o와 비교를 하고 a보다 큰 o를 오른쪽 하위노드에 삽입한다. 나머지 문자열 w는 가운데 하위노드에 삽입된다.

2.2 탐색

2.2.1 “car”키를 가진 데이터 탐색

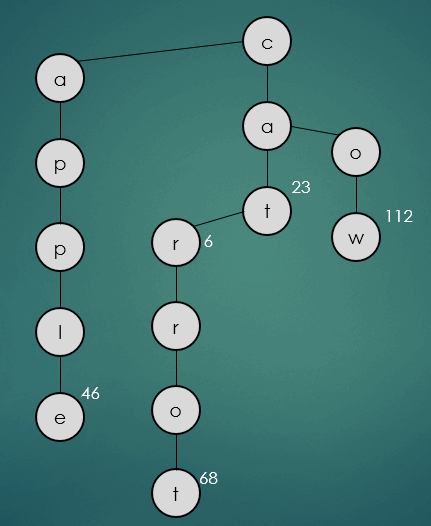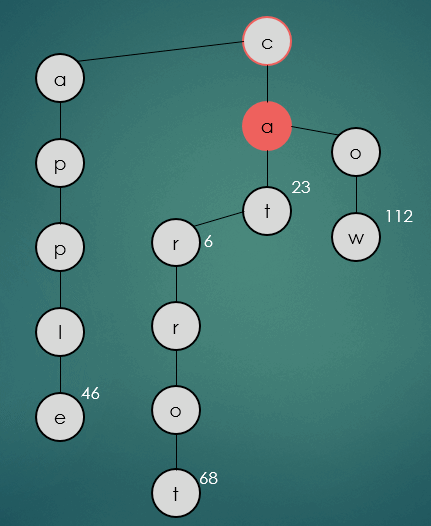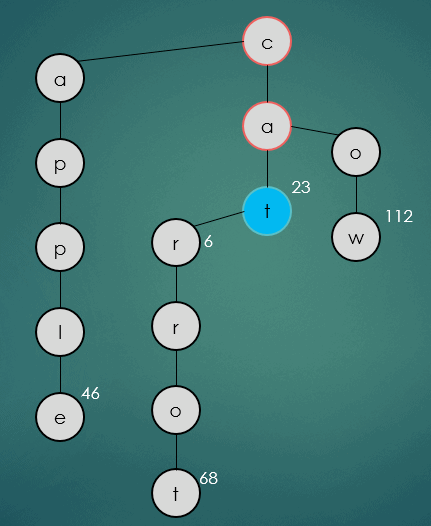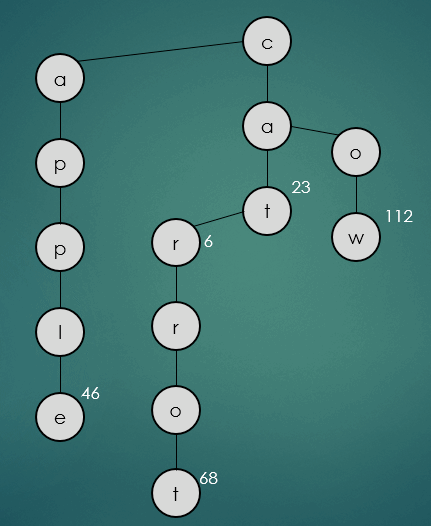
tst-get-car

get("car");

car을 탐색은 위와 같이 문자열을 하나씩 비교해가면서 동일한 경우 가운데 하위노드를 따라 이동한다. 만약 일치하지 않는 문자열을 만나게 되면 해당 문자열과 비교하여 작은 문자열인 경우 왼쪽, 큰 문자열 인 경우 오른쪽 하위노드로 이동한다.

2.2.2 일치하는 문자열이 존재하지 않을 경우

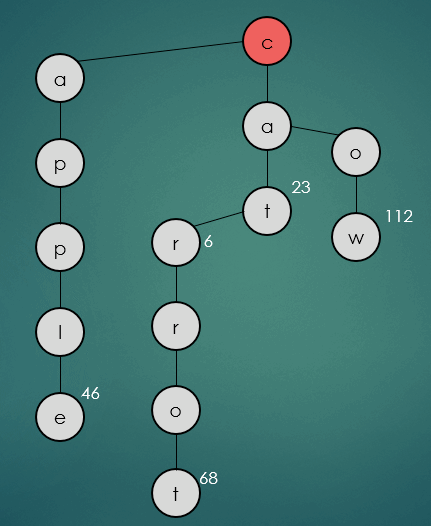
tst-get-d

get("dog");

일치하는 문자열이 존재하지 않을 경우 연산을 종료시킨다.

3 구현

3.1 클래스 작성

// 노드 클래스
public class Node {

    private char character;     // 문자
    private Node leftNode;      // LESS
    private Node middleNode;    // EQUAL
    private Node rightNode;     // GREATER
    private int value;          // 값

    // 생성자
    public Node(char character) {
        this.character = character;
    }

    // getter, setter

}

public class TST {

    private Node rootNode;

    // 삽입
    // 삽입 처리

    // 탐색
    // 탐색 처리
}

3.2 삽입 메서드

// 삽입
public void put(String key, int value) {

    rootNode = put(rootNode, key, value, 0);

}

// 삽입 처리
private Node put(Node node, String key, int value, int index) {

    char c = key.charAt(index); // 문자 추출

    // 현재 노드가 null 이면
    if (node == null) {
        node = new Node(c); // 새로운 노드 생성
    }

    // LESS : 추출한 문자 < 현재 노드의 문자
    if (c < node.getCharacter()) {
        // 왼쪽 하위노드로 세팅, 삽입 재귀호출
        node.setLeftNode(put(node.getLeftNode(), key, value, index));

    // GREATER : 추출한 문자열 > 현재 노드의 문자열
    } else if (c > node.getCharacter()) {
        // 오른쪽 하위노드로 세팅, 삽입 재귀 호출
        node.setRightNode(put(node.getRightNode(), key, value, index));

    // EQUAL : 현재 인덱스 < 전체 키의 길이
    } else if (index < key.length() - 1) {
        // 가운데 하위노드로 세팅, 삽입 재귀 호출(인덱스 1 증가)
        node.setMiddleNode(put(node.getMiddleNode(), key, value, index + 1));

    // 값 저장
    } else {
        node.setValue(value);
    }

    return node;
}

3.3 탐색 메서드

// 탐색
public Integer get(String key) {

    Node node = get(rootNode, key, 0);

    if (node == null) {
        return null;
    }

    return node.getValue();
}

// 탐색 처리
private Node get(Node node, String key, int index) {

    if (node == null) {
        return null;
    }

    char c = key.charAt(index); // 문자 추출

    // LESS : 추출한 문자 < 현재 노드의 문자
    if (c < node.getCharacter()) {
        // 왼쪽 하위노드 탐색 재귀 호출
        return get(node.getLeftNode(), key, index);

    // GREATER : 추출한 문자 > 현재 노드의 문자
    } else if (c > node.getCharacter()) {
        // 오른쪽 하위노드 탐색 재귀 호출
        return get(node.getRightNode(), key, index);

    // EQUAL : 현재 인덱스 < 전체 문자열의 길이
    } else if (index < key.length() - 1) {
        // 가운데 하위노드 탐색 재귀호출(인덱스 1증가)
        return get(node.getMiddleNode(), key, index + 1);

    // 값이 저장된 노드 반환
    } else {
        return node;
    }

}

3.4 테스트

public class App {
    public static void main(String[] args) {
        TST tst = new TST();
        tst.put("cat", 1);
        tst.put("apple", 2);
        tst.put("car", 3);
        tst.put("carrot", 4);
        tst.put("cow", 5);

        System.out.println(tst.get("car"));
        System.out.println(tst.get("carrot"));
        System.out.println(tst.get("cow"));
        System.out.println(tst.get("hello"));
    }
}

3
4
5
null

4. Reference

본 글은 Udemy의 자바 자료구조 강의를 듣고 개인적으로 학습한 내용 복습하기 위해 작성된 글로 내용상 오류가 있을 수 있습니다. 오류가 있다면 지적 부탁 드리겠습니다.

검색